一.认识数组 | KWAN的解忧杂货铺

# 一.认识数组

# 1.数组概述

定义:在计算机科学中，数组是由一组元素（值或变量）组成的数据结构，每个元素有至少一个索引或键来标识

因为数组内的元素是连续存储的，所以数组中元素的地址，可以通过其索引计算出来，例如：

int[] array = {1,2,3,4,5}

知道了数组的数据起始地址 $BaseAddress$，就可以由公式 $BaseAddress + i * size$ 计算出索引 $i$ 元素的地址

$i$ 即索引，在 Java、C 等语言都是从 0 开始
$size$ 是每个元素占用字节，例如 $int$ 占 $4$，$double$ 占 $8$

空间占用:

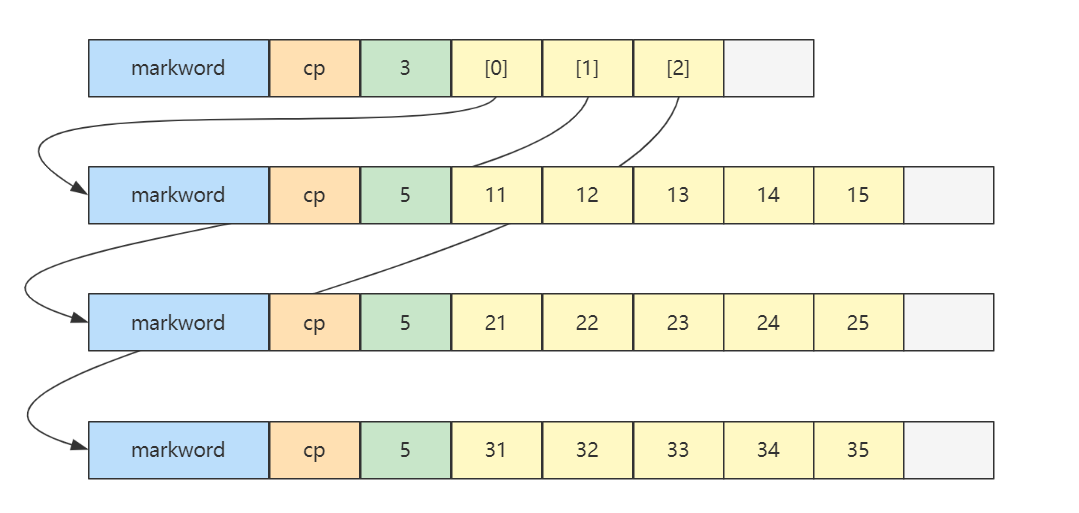
Java 中数组结构为

8 字节 markword
4 字节 class 指针（压缩 class 指针的情况）
4 字节数组大小（决定了数组最大容量是 $2^{32}$）
数组元素 + 对齐字节（java 中所有对象大小都是 8 字节的整数倍，不足的要用对齐字节补足）

例如

int[] array = {1, 2, 3, 4, 5};

数组的大小为 40 个字节，组成如下

8 + 4 + 4 + 5*4 + 4(alignment)

随机访问性能:即根据索引查找元素，时间复杂度是 $O(1)$

# 2.动态数组

public class DynamicArray implements Iterable<Integer> {
    private int size = 0; // 逻辑大小
    private int capacity = 8; // 容量
    private int[] array = {};


    /**
     * 向最后位置 [size] 添加元素
     *
     * @param element 待添加元素
     */
    public void addLast(int element) {
        add(size, element);
    }

    /**
     * 向 [0 .. size] 位置添加元素
     *
     * @param index   索引位置
     * @param element 待添加元素
     */
    public void add(int index, int element) {
        checkAndGrow();

        // 添加逻辑
        if (index >= 0 && index < size) {
            // 向后挪动, 空出待插入位置
            System.arraycopy(array, index,
                    array, index + 1, size - index);
        }
        array[index] = element;
        size++;
    }

    private void checkAndGrow() {
        // 容量检查
        if (size == 0) {
            array = new int[capacity];
        } else if (size == capacity) {
            // 进行扩容, 1.5 1.618 2
            capacity += capacity >> 1;
            int[] newArray = new int[capacity];
            System.arraycopy(array, 0,
                    newArray, 0, size);
            array = newArray;
        }
    }

    /**
     * 从 [0 .. size) 范围删除元素
     *
     * @param index 索引位置
     * @return 被删除元素
     */
    public int remove(int index) { // [0..size)
        int removed = array[index];
        if (index < size - 1) {
            // 向前挪动
            System.arraycopy(array, index + 1,
                    array, index, size - index - 1);
        }
        size--;
        return removed;
    }


    /**
     * 查询元素
     *
     * @param index 索引位置, 在 [0..size) 区间内
     * @return 该索引位置的元素
     */
    public int get(int index) {
        return array[index];
    }

    /**
     * 遍历方法1
     *
     * @param consumer 遍历要执行的操作, 入参: 每个元素
     */
    public void foreach(Consumer<Integer> consumer) {
        for (int i = 0; i < size; i++) {
            // 提供 array[i]
            // 返回 void
            consumer.accept(array[i]);
        }
    }

    /**
     * 遍历方法2 - 迭代器遍历
     */
    @Override
    public Iterator<Integer> iterator() {
        return new Iterator<Integer>() {
            int i = 0;

            @Override
            public boolean hasNext() { // 有没有下一个元素
                return i < size;
            }

            @Override
            public Integer next() { // 返回当前元素,并移动到下一个元素
                return array[i++];
            }
        };
    }

    /**
     * 遍历方法3 - stream 遍历
     *
     * @return stream 流
     */
    public IntStream stream() {
        return IntStream.of(Arrays.copyOfRange(array, 0, size));
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118

这些方法实现，都简化了 index 的有效性判断，假设输入的 index 都是合法的

插入或删除性能:

头部位置，时间复杂度是 $O(n)$

中间位置，时间复杂度是 $O(n)$

尾部位置，时间复杂度是 $O(1)$（均摊来说）

# 3.二维数组

int[][] array = {
    {11, 12, 13, 14, 15},
    {21, 22, 23, 24, 25},
    {31, 32, 33, 34, 35},
};

1
2
3
4
5

内存图如下

二维数组占 32 个字节，其中 array[0]，array[1]，array[2] 三个元素分别保存了指向三个一维数组的引用
三个一维数组各占 40 个字节
它们在内层布局上是连续的

更一般的，对一个二维数组 $Array[m][n]$

$m$ 是外层数组的长度，可以看作 row 行
$n$ 是内层数组的长度，可以看作 column 列
当访问 $Array[i][j]$，$0\leq i \lt m, 0\leq j \lt n$时，就相当于
- 先找到第 $i$ 个内层数组（行）
- 再找到此内层数组中第 $j$ 个元素（列）

小测试

Java 环境下（不考虑类指针和引用压缩，此为默认情况），有下面的二维数组

byte[][] array = {
    {11, 12, 13, 14, 15},
    {21, 22, 23, 24, 25},
    {31, 32, 33, 34, 35},
};

1
2
3
4
5

已知 array 对象起始地址是 0x1000，那么 23 这个元素的地址是什么？

答：

起始地址 0x1000

外层数组大小：16 字节对象头 + 3 元素 * 每个引用 4 字节 + 4 对齐字节 = 32 = 0x20

第一个内层数组大小：16 字节对象头 + 5 元素 * 每个 byte1 字节 + 3 对齐字节 = 24 = 0x18

第二个内层数组，16 字节对象头 = 0x10，待查找元素索引为 2

最后结果 = 0x1000 + 0x20 + 0x18 + 0x10 + 2*1 = 0x104a

# 4.局部性原理

这里只讨论空间局部性

cpu 读取内存（速度慢）数据后，会将其放入高速缓存（速度快）当中，如果后来的计算再用到此数据，在缓存中能读到的话，就不必读内存了
缓存的最小存储单位是缓存行（cache line），一般是 64 bytes，一次读的数据少了不划算啊，因此最少读 64 bytes 填满一个缓存行，因此读入某个数据时也会读取其临近的数据，这就是所谓空间局部性

对效率的影响:

比较下面 ij 和 ji 两个方法的执行效率

int rows = 1000000;
int columns = 14;
int[][] a = new int[rows][columns];

StopWatch sw = new StopWatch();
sw.start("ij");
ij(a, rows, columns);
sw.stop();
sw.start("ji");
ji(a, rows, columns);
sw.stop();
System.out.println(sw.prettyPrint());

1
2
3
4
5
6
7
8
9
10
11
12

ij 方法

public static void ij(int[][] a, int rows, int columns) {
    long sum = 0L;
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < columns; j++) {
            sum += a[i][j];
        }
    }
    System.out.println(sum);
}

1
2
3
4
5
6
7
8
9

ji 方法

public static void ji(int[][] a, int rows, int columns) {
    long sum = 0L;
    for (int j = 0; j < columns; j++) {
        for (int i = 0; i < rows; i++) {
            sum += a[i][j];
        }
    }
    System.out.println(sum);
}

1
2
3
4
5
6
7
8
9

执行结果

0
0
StopWatch '': running time = 96283300 ns
---------------------------------------------
ns         %     Task name
---------------------------------------------
016196200  017%  ij
080087100  083%  ji

1
2
3
4
5
6
7
8

可以看到 ij 的效率比 ji 快很多，为什么呢？

缓存是有限的，当新数据来了后，一些旧的缓存行数据就会被覆盖
如果不能充分利用缓存的数据，就会造成效率低下

以 ji 执行为例，第一次内循环要读入 $[0,0]$ 这条数据，由于局部性原理，读入 $[0,0]$ 的同时也读入了 $[0,1] ... [0,13]$，如图所示

但很遗憾，第二次内循环要的是 $[1,0]$ 这条数据，缓存中没有，于是再读入了下图的数据

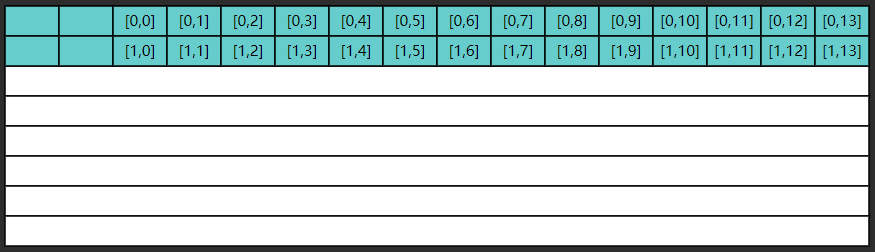
这显然是一种浪费，因为 $[0,1] ... [0,13]$ 包括 $[1,1] ... [1,13]$ 这些数据虽然读入了缓存，却没有及时用上，而缓存的大小是有限的，等执行到第九次内循环时

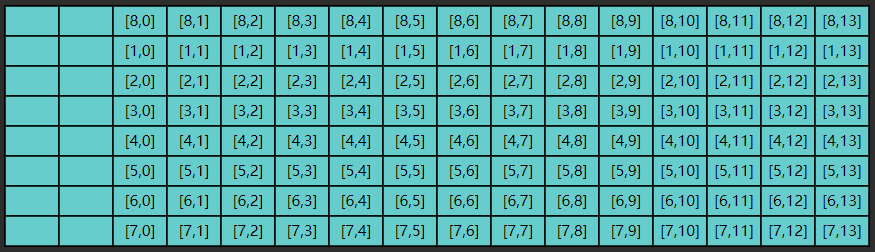
缓存的第一行数据已经被新的数据 $[8,0] ... [8,13]$ 覆盖掉了，以后如果再想读，比如 $[0,1]$，又得到内存去读了

同理可以分析 ij 函数则能充分利用局部性原理加载到的缓存数据

举一反三:

I/O 读写时同样可以体现局部性原理
数组可以充分利用局部性原理，那么链表呢？

答：链表不行，因为链表的元素并非相邻存储

# 5.越界检查

java 中对数组元素的读写都有越界检查，类似于下面的代码

bool is_within_bounds(int index) const
{
    return 0 <= index && index < length();
}

1
2
3
4

代码位置：openjdk\src\hotspot\share\oops\arrayOop.hpp

只不过此检查代码，不需要由程序员自己来调用，JVM 会帮我们调用

# 二.数组刷题

# 1.反转字符串 II-力扣 541 题

给定一个字符串 s 和一个整数 k，从字符串开头算起，每计数至 2k 个字符，就反转这 2k 字符中的前 k 个字符。

如果剩余字符少于 k 个，则将剩余字符全部反转。

如果剩余字符小于 2k 但大于或等于 k 个，则反转前 k 个字符，其余字符保持原样。

输入：s = "abcdefg", k = 2
输出："bacdfeg"

输入：s = "abcd", k = 2
输出："bacd"

1
2
3
4
5

public static void main(String[] args) {
    String a = "abcdefg";//bacdfeg
    E04ReverseStr541 e04ReverseStr541 = new E04ReverseStr541();
    String reverseStr = e04ReverseStr541.reverseStr(a, 2);
    System.out.println(reverseStr);
}

public String reverseStr(String s, int k) {
    final char[] chars = s.toCharArray();
    final int len = chars.length;
    for (int i = 0; i < len; i += 2 * k) {
        //起点是i,终点是i+k,或者是len,取小的,k取2,index取的是1
        reverse(chars, i, Math.min(i + k - 1, len - 1));
    }
    return String.valueOf(chars);
}

/**
 * 翻转char,翻转字符串
 *
 * @param chars
 * @param left
 * @param right
 */
private void reverse(char[] chars, int left, int right) {
    while (left < right) {
        char temp = chars[left];
        chars[left] = chars[right];
        chars[right] = temp;
        left++;
        right--;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

# 1.合并两个有序数组-力扣 88 题

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

1
2
3
4

题解

public void merge(int[] nums1, int m, int[] nums2, int n) {
    int j=m-1;
    int i=n-1;
    int k=m+n-1;
    while(j>=0&&i>=0){
        if(nums1[j]>nums2[i]){
            nums1[k--]=nums1[j--];
        }else{
            nums1[k--]=nums2[i--];
        }
    }
    while(i>=0){
           nums1[k--]=nums2[i--];
    }
    while(j>=0){
        nums1[k--]=nums1[j--];
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 2.寻找重复数-力扣 287 题

输入：nums = [1,3,4,2,2]
输出：2

1
2

题解

public int findDuplicate(int[] nums) {
    Arrays.sort(nums);
    for(int i=0;i<nums.length-1;i++){
        if(nums[i]==nums[i+1]){
            return nums[i];
        }
    }
    return -1;
}

1
2
3
4
5
6
7
8
9

# 1.两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那两个整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

1
2
3

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

1
2

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

1
2

题解:

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        map={}
        for index,num in enumerate(nums):
            map[num]=index
        for i,num in  enumerate(nums):
            num2=target-num
            j=map.get(num2)
            if j is not None and j!=i:
                return [i,j]

1
2
3
4
5
6
7
8
9
10

# 2.删除有序数组中的重复项

给你一个升序排列的数组 nums ，请你原地删除重复出现的元素，使每个元素只出现一次，返回删除后数组的新长度。元素的相对顺序应该保持一致。然后返回 nums 中唯一元素的个数。

考虑 nums 的唯一元素的数量为 k ，你需要做以下事情确保你的题解可以被通过：

更改数组 nums ，使 nums 的前 k 个元素包含唯一元素，并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。返回 k 。判题标准:

系统会用下面的代码来测试你的题解:

int[] nums = [...]; // 输入数组 int[] expectedNums = [...]; // 长度正确的期望答案

int k = removeDuplicates(nums); // 调用

assert k == expectedNums.length; for (int i = 0; i < k; i++) { assert nums[i] == expectedNums[i]; } 如果所有断言都通过，那么您的题解将被通过

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2,_]

1
2

解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。 示例 2：

输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]

1
2

解释：函数应该返回新的长度 5 ，并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

题解:

核心思路是使用双指针，一个指针 i 遍历数组，另一个指针 k 指向不重复的位置。当 nums[i] != nums[i-1] 时，说明当前元素不重复，将其赋值给 nums[k]，然后将 k 加 1。最后返回 k 即可。时间复杂度为 O(n)，空间复杂度为 O(1)。

class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:
        if not nums:
            return 0
        k=1
        for i in range(1,len(nums)):
            if nums[i]!=nums[i-1]:
                nums[k]=nums[i]
                k+=1
        return k

1
2
3
4
5
6
7
8
9
10

# 3.移除元素

给你一个数组 nums 和一个值 val，你需要 原地 (opens new window) 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 (opens new window)修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]
解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。

1
2
3

示例 2：

输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3]
解释：函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。

1
2
3

题解:

from typing import List


class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        """
        左指针 单指针遍历
        :param nums:
        :param val:
        :return:
        """
        left = 0
        for index in range(0, len(nums)):
            if nums[index] != val:
                nums[left] = nums[index]
                left += 1
        return left

    def removeElement2(self, nums: List[int], val: int) -> int:
        """
        双指针优化,左右夹逼
        :param nums:
        :param val:
        :return:
        """
        left = 0
        right = len(nums)
        while left < right:
            if nums[left] == val:
                nums[left] = nums[right - 1]
                right -= 1
            else:
                left += 1
        return left


if __name__ == '__main__':
    result = Solution().removeElement2([2], 3)
    print(result)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

# 5.加一

给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位，数组中每个元素只存储单个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

示例 1：

输入：digits = [1,2,3]
输出：[1,2,4]
解释：输入数组表示数字 123。

1
2
3

示例 2：

输入：digits = [4,3,2,1]
输出：[4,3,2,2]
解释：输入数组表示数字 4321。

1
2
3

示例 3：

输入：digits = [0]
输出：[1]

1
2

题解:

from typing import List
class Solution:
    def plusOne(self, digits: List[int]) -> List[int]:
        """
        加一
        :param digits:
        :return:
        """
        if not digits:
            return None
        s = ''
        res = []
        for value in digits:
            s = s + str(value)
        for i in str(int(s) + 1):
            res.append(int(i))
        return res

    def plusOne2(self, digits: List[int]) -> List[int]:
        """
        解法一的一行写法
        :param digits:
        :return:
        """
        return [int(i) for i in str(int(''.join([str(j) for j in digits])) + 1)]

    def plusOne3(self, digits: List[int]) -> List[int]:
        """
        常规解法
        :param digits:
        :return:
        """
        plus = 1
        for i in range(len(digits) - 1, -1, -1):
            if digits[i] + plus == 10:
                digits[i] = 0
                plus = 1
            else:
                digits[i] += plus
                plus = 0
        if plus == 1:
            digits.insert(0, 1)
        return digits

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

# 6.合并两个有序数组

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

**注意：**最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

1
2
3
4

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 。
合并结果是 [1] 。

1
2
3
4

示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。

1
2
3
4
5

题解:

这个函数的输入参数包括两个有序数组 nums1 和 nums2，以及它们各自的长度 m 和 n。函数的输出是将两个数组合并后的结果，存储在 nums1 数组中。

这个函数使用了三个指针 i、j 和 k，分别指向 nums1 中最后一个有值的元素、nums2 中最后一个有值的元素和 nums1 中最后一个元素的位置。然后从后往前遍历 nums1 和 nums2，将较大的元素放到 nums1 的末尾。最后如果 nums2 中还有元素未放入 nums1 中，直接放到 nums1 的前面。

class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        先填充后面的,再填充前面的
        """
        if not nums2:
            return
        len1 = m - 1  # nums1的最后的索引
        len2 = n - 1  # nums2的最后的索引
        k = m + n - 1 # 合并后的最后的索引
        # 从后向前遍历 nums1 和 nums2，将较大的元素放到 nums1 的末尾
        while len1 >= 0 and len2 >= 0:
            if nums1[len1] > nums2[len2]:
                nums1[k] = nums1[len1]
                len1 -= 1
            else:
                nums1[k] = nums2[len2]
                len2 -= 1
            k -= 1
        # 如果 nums2 中还有元素未放入 nums1 中，直接放到 nums1 的前面
        if len2 >= 0:
            # 切片赋值,切片是不包含尾部的
            nums1[:len2 + 1] = nums2[:len2 + 1]
        return nums1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 7.将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

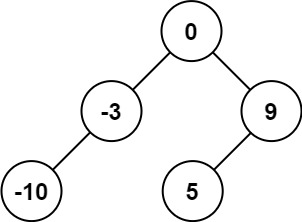
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

1
2
3

示例 2：

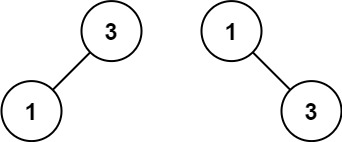
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

1
2
3

题解:

实现了将有序数组转换为二叉搜索树。该算法的基本思想是：

选择中间的元素作为根节点，可以将数组分为左右两个子数组；
左子数组中的元素小于根节点，右子数组中的元素大于根节点；
递归处理左右子数组。

这样构建的二叉搜索树满足以下性质：

根节点的值等于中间元素的值；
左子树是由左半部分元素构成的二叉搜索树；
右子树是由右半部分元素构成的二叉搜索树。

from typing import List, Optional


class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
        if not nums:
            return None
        mid = (len(nums)) // 2
        root = TreeNode(nums[mid])
        root.left = self.sortedArrayToBST(nums[:mid])
        root.right = self.sortedArrayToBST(nums[mid + 1:])
        return root


if __name__ == '__main__':
    nums = [-10, -3, 0, 5, 9]
    root = Solution().sortedArrayToBST(nums)
    print(root)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

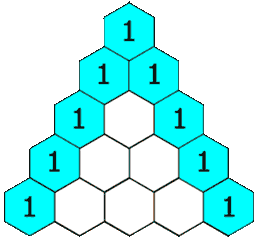
# 8.杨辉三角

给定一个非负整数 *numRows，*生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

1
2

示例 2:

输入: numRows = 1
输出: [[1]]

1
2

题解:

该算法的基本思想是：

第一行只有一个元素 1；
第 i 行有 i 个元素；
每一行的第一个和最后一个元素都为 1；
每个元素等于上一行中与其相邻的两个元素之和。

例如，杨辉三角的前 5 行如下所示：

1
2
3
4
5

以上代码中，使用一个二维列表 result 来存储杨辉三角的所有元素。在循环中，首先创建一个长度为 i+1 的列表 row，并将其所有元素初始化为 1，然后通过遍历上一行的元素来计算当前行的元素，并将其存入 row 列表中。最后将 row 添加到 result 列表中，即可生成下一行杨辉三角的元素。

class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        """
        杨辉三角
        第一行只有一个元素 1；
        第 i 行有 i 个元素；
        每一行的第一个和最后一个元素都为 1；
        每个元素等于上一行中与其相邻的两个元素之和。
        :param numRows:
        :return:
        """
        if numRows == 0:
            return []
        result = [[1]]
        for i in range(1, numRows):
            # 当前行全为1
            row = [1] * (i + 1)
            # 只需要修改第二个和倒数第二个的值
            for j in range(1, i):
                # 值为上一行的左右2数相加
                row[j] = result[i - 1][j - 1] + result[i - 1][j]
            result.append(row)
        return result


if __name__ == '__main__':
    root = Solution().generate(5)
    print(root)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# 9.杨辉三角 II

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例 1:

输入: rowIndex = 3
输出: [1,3,3,1]

1
2

示例 2:

输入: rowIndex = 0
输出: [1]

1
2

示例 3:

输入: rowIndex = 1
输出: [1,1]

1
2

题解:

class Solution:
    def getRow(self, rowIndex: int) -> List[int]:
        """
        索引从index=0开始
        :param rowIndex:
        :return:
        """
        if rowIndex == 0:
            return [1]
        result = [[1]]
        # range(1,1)不走遍历,所以要加1
        for i in range(1, rowIndex + 1):
            row = [1] * (i + 1)
            for j in range(1, i):
                row[j] = result[i - 1][j - 1] + result[i - 1][j]
            # 外层等于rowIndex即可结束遍历
            if i == rowIndex:
                return row
            result.append(row)


if __name__ == '__main__':
    root = Solution().getRow(4)
    print(root)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# 10.买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

1
2
3
4

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

1
2
3

题解:

该算法的基本思想是：

遍历股票价格列表，记录当天之前的最低价格 min_price 和最大收益 max_profit；
对于每一天的价格，如果低于 min_price，则更新 min_price；否则计算当天的收益，并更新 max_profit。

例如，对于价格列表 [7, 1, 5, 3, 6, 4]，最佳时机是在第二天买入价格为 1 的股票，第五天卖出价格为 6 的股票，可以获得最大收益 5。

以上代码中，使用 min_price 记录当天之前的最低价格，使用 max_profit 记录当前的最大收益。在遍历股票价格列表时，如果当天的价格低于 min_price，则更新 min_price；否则计算当天的收益，并更新 max_profit 为当前收益和历史最大收益的较大值。最后返回最大收益即可。

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        """
        贪心算法
        2个变量,一个最小价格,一个最大利润
        :param prices:
        :return:
        """
        min_price = prices[0]
        max_profit = 0
        for i in range(1, len(prices)):
            if prices[i] < min_price:
                min_price = prices[i]
            else:
                max_profit = max(max_profit, prices[i] - min_price)
        return max_profit


if __name__ == '__main__':
    root = Solution().maxProfit([7, 1, 5, 3, 6, 4])
    print(root)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# 11.只出现一次的数字

给你一个非空整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

示例 1 ：

输入：nums = [2,2,1]
输出：1

1
2

示例 2 ：

输入：nums = [4,1,2,1,2]
输出：4

1
2

示例 3 ：

输入：nums = [1]
输出：1

1
2

题解:

以下代码实现了求解只出现一次的数字。该算法的基本思想是使用位运算中的异或操作（^）：

对于两个相同的数字，它们的二进制位全部相同，异或后结果为 0；
对于两个不同的数字，它们的二进制位至少有一位不同，异或后结果为 1。

因此，对于一个数组中只出现一次的数字，将所有数字进行异或操作后，最终的结果就是该数字本身。

例如，对于数组 [2, 2, 1]，异或操作的结果为 2 ^ 2 ^ 1 = 1，因此只出现一次的数字是 1。

以上代码中，使用 result 变量来记录异或操作的结果。在遍历数组时，对于每个数字，将其与 result 进行异或操作，最终得到的 result 就是只出现一次的数字。

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        """
        异或运算
        :param nums:
        :return:
        """
        result = 0
        for i in nums:
            result ^= i
        return result

1
2
3
4
5
6
7
8
9
10
11

# 12.多数元素

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1：

输入：nums = [3,2,3]
输出：3

1
2

示例 2：

输入：nums = [2,2,1,1,1,2,2]
输出：2

1
2

题解:

多数元素指的是在一个数组中出现次数超过数组长度一半的元素。可以使用摩尔投票算法（Moore Voting Algorithm）来解决该问题，该算法的时间复杂度为 O(n)。

该算法通过遍历数组，维护一个候选元素和一个计数器。初始化时，候选元素为空，计数器为 0。遍历数组时，如果计数器为 0，则将当前元素设置为候选元素；如果当前元素等于候选元素，则计数器加 1，否则计数器减 1。遍历结束后，候选元素即为多数元素。

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        """
        多数元素
        :param nums:
        :return:
        """
        count = 0
        candidate = None
        for i in nums:
            if count == 0:
                candidate = i
            if i == candidate:
                count += 1
            else:
                count += -1
        return candidate

    def majorityElement2(self, nums: List[int]) -> int:
        """
        多数元素
        :param nums:
        :return:
        """
        count = 0
        candidate = None
        for i in nums:
            if count == 0:
                candidate = i
            count += (1 if i == candidate else -1)
        return candidate

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# 13.存在重复元素

给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ，返回 true ；如果数组中每个元素互不相同，返回 false 。

示例 1：

输入：nums = [1,2,3,1]
输出：true

1
2

示例 2：

输入：nums = [1,2,3,4]
输出：false

1
2

示例 3：

输入：nums = [1,1,1,3,3,4,3,2,4,2]
输出：true

1
2

题解:

判断一个数组中是否存在重复元素，可以使用 Python 中的 set 集合数据类型。set 可以在 O(1)的时间复杂度内判断元素是否存在，因此可以使用 set 来判断数组中是否存在重复元素。

首先将数组转换为 set，然后判断 set 的长度是否等于原数组的长度，如果不相等，则说明原数组中存在重复元素。

class Solution:
    def containsDuplicate(self, nums: List[int]) -> bool:
        """
        set集合去重
        :param nums:
        :return:
        """
        new_list = set(nums)
        return len(new_list) != len(nums)

1
2
3
4
5
6
7
8
9

# 14.存在重复元素 II

给你一个整数数组 nums 和一个整数 k ，判断数组中是否存在两个 不同的索引 i 和 j ，满足 nums[i] == nums[j] 且 abs(i - j) <= k 。如果存在，返回 true ；否则，返回 false 。

示例 1：

输入：nums = [1,2,3,1], k = 3
输出：true

1
2

示例 2：

输入：nums = [1,0,1,1], k = 1
输出：true

1
2

示例 3：

输入：nums = [1,2,3,1,2,3], k = 2
输出：false

1
2

题解:

判断一个数组中是否存在两个相同的元素，它们的下标差不超过 k，可以使用滑动窗口和哈希表来解决该问题。使用一个大小为 k 的滑动窗口，在遍历数组时，将每个元素的值作为键，将下标作为值存储在哈希表中。如果当前元素的值已经在哈希表中存在，则判断当前下标和哈希表中该元素的下标之差是否不超过 k，如果是，则说明满足条件，返回 True 即可。

遍历数组，将每个元素的值作为键，将下标作为值存储在哈希表中。如果当前元素的值已经在哈希表中存在，则判断当前下标和哈希表中该元素的下标之差是否不超过 k，如果是，则说明满足条件，返回 True 即可。如果遍历完整个数组都没有返回 True，则说明不存在两个相同的元素，它们的下标差不超过 k，返回 False 即可。

class Solution:
    def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:
        """
        基础暴力破解,超出时间限制
        :param nums:
        :param k:
        :return:
        """
        for i, i_val in enumerate(nums):
            for j, j_val in enumerate(nums):
                if i != j and i_val == j_val and abs(i - j) <= k:
                    return True
        return False

    def containsNearbyDuplicate1(self, nums: List[int], k: int) -> bool:
        """
        字典的使用
        :param nums:
        :param k:
        :return:
        """
        num_dict = {}
        for i, num in enumerate(nums):
            # 关键判断
            if num in num_dict and i - num_dict.get(num) <= k:
                return True
            else:
                num_dict[num] = i
        return False

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# 15.汇总区间

给定一个 无重复元素 的有序整数数组 nums 。

返回 *恰好覆盖数组中所有数字的 最小有序 区间范围列表* 。也就是说，nums 的每个元素都恰好被某个区间范围所覆盖，并且不存在属于某个范围但不属于 nums 的数字 x 。

列表中的每个区间范围 [a,b] 应该按如下格式输出：

"a->b" ，如果 a != b

"a" ，如果 a == b

示例 1：

输入：nums = [0,1,2,4,5,7]
输出：["0->2","4->5","7"]
解释：区间范围是：
[0,2] --> "0->2"
[4,5] --> "4->5"
[7,7] --> "7"

1
2
3
4
5
6

示例 2：

输入：nums = [0,2,3,4,6,8,9]
输出：["0","2->4","6","8->9"]
解释：区间范围是：
[0,0] --> "0"
[2,4] --> "2->4"
[6,6] --> "6"
[8,9] --> "8->9"

1
2
3
4
5
6
7

题解:

def getRange(start, end):
    if start == end:
        return str(start)
    else:
        return str(start) + '->' + str(end)

class Solution:
    def summaryRanges(self, nums: List[int]) -> List[str]:
        """
        数组变量,差值不为1,则特殊处理
        :param nums:
        :return:
        """
        if not nums:
            return []
        result = []
        start = nums[0]
        for i in range(1, len(nums)):
            if nums[i] != nums[i - 1] + 1:
                result.append(getRange(start, nums[i - 1]))
                start = nums[i]
        result.append(getRange(start, nums[-1]))
        return result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 16.丢失的数字

给定一个包含 [0, n] 中 n 个数的数组 nums ，找出 [0, n] 这个范围内没有出现在数组中的那个数。

示例 1：

输入：nums = [3,0,1]
输出：2
解释：n = 3，因为有 3 个数字，所以所有的数字都在范围 [0,3] 内。2 是丢失的数字，因为它没有出现在 nums 中。

1
2
3

示例 2：

输入：nums = [0,1]
输出：2
解释：n = 2，因为有 2 个数字，所以所有的数字都在范围 [0,2] 内。2 是丢失的数字，因为它没有出现在 nums 中。

1
2
3

示例 3：

输入：nums = [9,6,4,2,3,5,7,0,1]
输出：8
解释：n = 9，因为有 9 个数字，所以所有的数字都在范围 [0,9] 内。8 是丢失的数字，因为它没有出现在 nums 中。

1
2
3

题解:

这个解法的思路是通过计算 0 到 n 的总和，然后减去实际数组的总和，就可以得到缺失的数字。需要注意的是，需要将计算结果转为整数类型。

class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        nums.sort()
        if nums[0] != 0:
            return 0
        for i in range(1, len(nums)):
            if nums[i] - nums[i - 1] > 1:
                return nums[i] - 1
        return nums[-1] + 1

    def missingNumber2(self, nums: List[int]) -> int:
        """
        主技巧  数学相关,求0到n的和
        :param nums:
        :return:
        """
        total = len(nums) * (len(nums) + 1) / 2
        sum_num = sum(nums)
        return int(total - sum_num)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# 17.移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例 1:

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

1
2

示例 2:

输入: nums = [0]
输出: [0]

1
2

题解:

这个解法的思路是通过定义两个指针 i 和 j，然后遍历数组。当遇到非零元素时，将其移动到数组的前面，然后指针 i 加 1。最后将剩余的位置都填充 0 即可。

需要注意的是，题目要求在原数组上进行操作，因此不能新建一个数组。

class Solution:
    def moveZeroes(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        i = 0
        j = 0
        while j < len(nums):
            if nums[j] != 0:
                nums[i] = nums[j]
                i += 1
            j += 1
        for index in range(i, len(nums)):
            nums[index] = 0
        print(nums)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 18.区域和检索 - 数组不可变

给定一个整数数组 nums，处理以下类型的多个查询:

计算索引 left 和 right （包含 left 和 right）之间的 nums 元素的和，其中 left <= right

实现 NumArray 类：

NumArray(int[] nums) 使用数组 nums 初始化对象

int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的总和，包含 left 和 right 两点（也就是 nums[left] + nums[left + 1] + ... + nums[right] )

示例 1：

输入：
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出：
[null, 1, -1, -3]

解释：
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1))
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))

1
2
3
4
5
6
7
8
9
10
11

题解:

class NumArray:

    def __init__(self, nums: List[int]):
        self.nums = nums

    def sumRange(self, left: int, right: int) -> int:
        """
        切片  求和
        :param left:
        :param right:
        :return:
        """
        return sum(self.nums[left: right + 1])

1
2
3
4
5
6
7
8
9
10
11
12
13

class NumArray:

    def __init__(self, nums: List[int]):
        self.nums = nums
        for i in range(1, len(nums)):
            # 前缀和
            self.nums[i] += self.nums[i - 1]

    def sumRange(self, left: int, right: int) -> int:
        """
        切片  求和
        :param left:
        :param right:
        :return:
        """
        if left == 0:
            return self.nums[right]
        return self.nums[right] - self.nums[left - 1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 19.两个数组的交集

给定两个数组 nums1 和 nums2 ，返回 它们的交集 。输出结果中的每个元素一定是唯一的。我们可以 不考虑输出结果的顺序 。

示例 1：

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2]

1
2

示例 2：

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[9,4]
解释：[4,9] 也是可通过的

1
2
3

题解:

使用 Python 中内置的 set 类型来求两个数组的交集。具体步骤如下：

将两个数组转化为 set 类型。
调用 set 类型的 intersection() 方法求交集。
将交集转化为 list 类型（如果需要）。

class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
        return list(set(nums1).intersection(nums2))

1
2
3

注意，使用 & 运算符求交集时，需要将 set 类型转化为 list 类型。

class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
        list1 = set(nums1)
        list2 = set(nums2)
        return list(list1 & list2)

1
2
3
4
5

迭代遍历

class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
        result = []
        for i in nums1:
            if i in nums2 and i not in result:
                result.append(i)
        return result
     def  intersection2(self, nums1: List[int], nums2: List[int]) -> List[int]:
     result = [i for i in list1 if i in list2]

1
2
3
4
5
6
7
8
9

# 20.两个数组的交集 II

给你两个整数数组 nums1 和 nums2 ，请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数，应与元素在两个数组中都出现的次数一致（如果出现次数不一致，则考虑取较小值）。可以不考虑输出结果的顺序。

示例 1：

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2,2]

1
2

示例 2:

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[4,9]

1
2

题解:

使用一个字典来记录一个数组中每个数字出现的次数，然后遍历另一个数组，如果当前数字在字典中出现次数大于 0，则将该数字添加到结果中，并将字典中记录的该数字出现次数减 1。

这个算法的时间复杂度为 O(m+n)，其中 m 和 n 分别为两个数组的长度，因为需要遍历两个数组，以及遍历字典中的所有数字。空间复杂度为 O(m)，因为需要使用字典来记录第一个数组中每个数字出现的次数。

class Solution:
    def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:
        dict1 = {}
        # 统计nums1中的各个数字个数
        for i in nums1:
            if i in dict1:
                dict1[i] += 1
            else:
                dict1[i] = 1
        res = []
        for num in nums2:
            if num in dict1 and dict1[num] > 0:
                res.append(num)
                dict1[num] -= 1
        return res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 21.第三大的数

给你一个非空数组，返回此数组中 第三大的数 。如果不存在，则返回数组中最大的数。

示例 1：

输入：[3, 2, 1]
输出：1
解释：第三大的数是 1 。

1
2
3

示例 2：

输入：[1, 2]
输出：2
解释：第三大的数不存在, 所以返回最大的数 2 。

1
2
3

示例 3：

输入：[2, 2, 3, 1]
输出：1
解释：注意，要求返回第三大的数，是指在所有不同数字中排第三大的数。
此例中存在两个值为 2 的数，它们都排第二。在所有不同数字中排第三大的数为 1 。

1
2
3
4

题解:

首先对列表进行去重并按降序排序，然后返回第三个元素，如果列表中元素个数不足 3 个，则返回提示信息。在上述示例中，输出结果为 5，因为第三大的数是 5。

class Solution:
    def thirdMax(self, nums: List[int]) -> int:
        if not nums:
            return None
        if len(nums) < 3:
            return max(nums)
        nums = sorted(set(nums), reverse=True)  # 去重并按降序排序
        if len(nums) >= 3:
            return nums[2]
        else:
            return nums[0]

1
2
3
4
5
6
7
8
9
10
11

# 22.找到所有数组中消失的数字

给你一个含 n 个整数的数组 nums ，其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字，并以数组的形式返回结果。

示例 1：

输入：nums = [4,3,2,7,8,2,3,1]
输出：[5,6]

1
2

示例 2：

输入：nums = [1,1]
输出：[2]

1
2

题解:

使用 set 集合的 difference 方法取差集

class Solution:
    def findDisappearedNumbers(self, nums: List[int]) -> List[int]:
        all = set([i + 1 for i in range(len(nums))])
        return list(all.difference(set(nums)))

1
2
3
4

# 23.分发饼干

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例 1:

输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

1
2
3
4
5
6

示例 2:

输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

1
2
3
4
5
6

题解:

class Solution:
    def findContentChildren(self, g: List[int], s: List[int]) -> int:
        g.sort()
        s.sort()
        i = 0
        j = 0
        count = 0
        while i < len(g) and j < len(s):
            if g[i] <= s[j]:
                count += 1
                i += 1
            j += 1
        return count

1
2
3
4
5
6
7
8
9
10
11
12
13

# 24.岛屿周长

给定一个 row x col 的二维网格地图 grid ，其中：grid[i][j] = 1 表示陆地， grid[i][j] = 0 表示水域。

网格中的格子 水平和垂直 方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

示例 1：

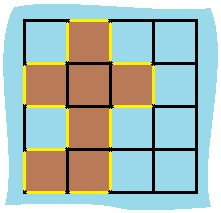
输入：grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
输出：16
解释：它的周长是上面图片中的 16 个黄色的边

1
2
3

示例 2：

输入：grid = [[1]]
输出：4

1
2

示例 3：

输入：grid = [[1,0]]
输出：4

1
2

题解:

class Solution:
    def islandPerimeter(self, grid: List[List[int]]) -> int:
        # x轴和y轴
        directions = [[0, 1], [0, -1], [1, 0], [-1, 0]]
        result = 0
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                # 如果是水域直接跳过,只处理岛屿的格子
                if grid[i][j] == 1:
                    # 存在岛屿则重置
                    count = 0
                    # 计算每个岛屿右左上下是否有水域或者是边界
                    for x, y in directions:
                        ix = i + x
                        jy = j + y
                        # 和岛屿连接的水域边,针对的是当前行的加减,当前行的坐标小于0或者大于等于最大index则说明是在边界
                        if ix < 0 or ix >= len(grid) or jy < 0 or jy >= len(grid[0]) or grid[ix][jy] == 0:
                            count += 1
                    result += count
        return result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# 25.最大连续 1 的个数

给定一个二进制数组 nums ，计算其中最大连续 1 的个数。

示例 1：

输入：nums = [1,1,0,1,1,1]
输出：3
解释：开头的两位和最后的三位都是连续 1 ，所以最大连续 1 的个数是 3.

1
2
3

示例 2:

输入：nums = [1,0,1,1,0,1]
输出：2

1
2

题解:

class Solution:
    def findMaxConsecutiveOnes(self, nums: List[int]) -> int:
        """
        贪心算法
        :param nums:
        :return:
        """
        res = 0
        count = 0
        for num in nums:
            if num == 0:
                count = 0
                continue
            count += 1
            res = max(res, count)
        return res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 26.提莫攻击

在《英雄联盟》的世界中，有一个叫 “提莫” 的英雄。他的攻击可以让敌方英雄艾希（编者注：寒冰射手）进入中毒状态。

当提莫攻击艾希，艾希的中毒状态正好持续 duration 秒。

正式地讲，提莫在 t 发起攻击意味着艾希在时间区间 [t, t + duration - 1]（含 t 和 t + duration - 1）处于中毒状态。如果提莫在中毒影响结束前再次攻击，中毒状态计时器将会重置，在新的攻击之后，中毒影响将会在 duration 秒后结束。

给你一个 非递减 的整数数组 timeSeries ，其中 timeSeries[i] 表示提莫在 timeSeries[i] 秒时对艾希发起攻击，以及一个表示中毒持续时间的整数 duration 。

返回艾希处于中毒状态的总秒数。

示例 1：

输入：timeSeries = [1,4], duration = 2
输出：4
解释：提莫攻击对艾希的影响如下：
- 第 1 秒，提莫攻击艾希并使其立即中毒。中毒状态会维持 2 秒，即第 1 秒和第 2 秒。
- 第 4 秒，提莫再次攻击艾希，艾希中毒状态又持续 2 秒，即第 4 秒和第 5 秒。
艾希在第 1、2、4、5 秒处于中毒状态，所以总中毒秒数是 4 。

1
2
3
4
5
6

示例 2：

输入：timeSeries = [1,2], duration = 2
输出：3
解释：提莫攻击对艾希的影响如下：
- 第 1 秒，提莫攻击艾希并使其立即中毒。中毒状态会维持 2 秒，即第 1 秒和第 2 秒。
- 第 2 秒，提莫再次攻击艾希，并重置中毒计时器，艾希中毒状态需要持续 2 秒，即第 2 秒和第 3 秒。
艾希在第 1、2、3 秒处于中毒状态，所以总中毒秒数是 3 。

1
2
3
4
5
6

题解:

解题思路：我们可以使用贪心算法来解决这道题。我们可以遍历整个时间序列 timeSeries，对于每个时间点，计算提莫对艾希的攻击持续时间，如果该攻击与之前的攻击有重叠部分，则将重叠部分的时间减去，使得艾希没有重复中毒的时间。最后，我们可以返回艾希处于中毒状态的总秒数

class Solution:
    def findPoisonedDuration(self, timeSeries: List[int], duration: int) -> int:
        """
        贪心算法
        :param timeSeries:
        :param duration:
        :return:
        """
        if not timeSeries:
            return 0
        res = duration
        for i in range(1, len(timeSeries)):
            # 中毒时间取最小值,当有重叠时timeSeries[i] - timeSeries[i - 1]
            res += min(duration, timeSeries[i] - timeSeries[i - 1])
        return res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 27.下一个更大元素 I

nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置右侧的 第一个 比 x 大的元素。

给你两个 没有重复元素 的数组 nums1 和 nums2 ，下标从 0 开始计数，其中nums1 是 nums2 的子集。

对于每个 0 <= i < nums1.length ，找出满足 nums1[i] == nums2[j] 的下标 j ，并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素，那么本次查询的答案是 -1 。

返回一个长度为 nums1.length 的数组 ans 作为答案，满足 ans[i] 是如上所述的 下一个更大元素 。

示例 1：

输入：nums1 = [4,1,2], nums2 = [1,3,4,2].
输出：[-1,3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：
- 4 ，用加粗斜体标识，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。
- 1 ，用加粗斜体标识，nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ，用加粗斜体标识，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。

1
2
3
4
5
6

示例 2：

输入：nums1 = [2,4], nums2 = [1,2,3,4].
输出：[3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：
- 2 ，用加粗斜体标识，nums2 = [1,2,3,4]。下一个更大元素是 3 。
- 4 ，用加粗斜体标识，nums2 = [1,2,3,4]。不存在下一个更大元素，所以答案是 -1 。

1
2
3
4
5

题解:

常规解法

class Solution:
    def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
        res = []
        for num in nums1:
            for index, num2 in enumerate(nums2):
                if num == num2:
                    flag = False
                    for right in range(index + 1, len(nums2)):
                        if right == len(nums2):
                            break
                        if nums2[right] > num2:
                            res.append(nums2[right])
                            flag = True
                            break
                    if flag:
                        break
                    res.append(-1)
        return res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

栈解法

解题思路:这道题可以使用栈的方法进行解决。我们可以使用一个栈 stack 来记录 nums2 中的元素，同时使用一个字典 next_map 来记录每个元素的下一个更大元素。我们可以从后向前遍历 nums2 中的元素，

如果当前元素大于栈顶元素,则我们可以弹出栈顶元素,直至栈顶元素大于等于当前元素,并将其下一个更大元素设置为当前栈顶元素。不存在则设置为-1.并将当前元素入栈；

最后，我们可以遍历 nums1 中的元素，并在 next_map 中查找其下一个更大元素，如果不存在则将其设置为 -1。

class Solution:
    def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
        """
        使用栈解决
        栈顶元素肯定是比当前元素大的元素,否则取出,stack=[4,3,1] 2在遍历4的时候取出了
        :param nums1:
        :param nums2:
        :return:
        """
        stack = []
        next_map = {}
        res = []

        # 倒序遍历nums2
        for num in nums2[::-1]:
            while stack and stack[-1] < num:
                stack.pop()
            next_map[num] = stack[-1] if stack else -1
            stack.append(num)
        for num in nums1:
            res.append(next_map[num])
        return res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

这段代码首先定义了一个栈 stack 和一个字典 next_map。然后从后向前遍历 nums2 中的元素，如果当前元素小于等于栈顶元素，则将其入栈；否则，我们可以弹出栈顶元素，并将其下一个更大元素设置为当前的栈顶元素。最后，我们遍历 nums1 中的元素，并在 next_map 中查找其下一个更大元素，如果不存在则将其设置为 -1。最终返回 res 列表，它包含了每个元素在 nums2 中的下一个比其大的值。

# 28.键盘行

给你一个字符串数组 words ，只返回可以使用在 美式键盘 同一行的字母打印出来的单词。键盘如下图所示。

美式键盘 中：

第一行由字符 "qwertyuiop" 组成。

第二行由字符 "asdfghjkl" 组成。

第三行由字符 "zxcvbnm" 组成。

示例 1：

输入：words = ["Hello","Alaska","Dad","Peace"]
输出：["Alaska","Dad"]

1
2

示例 2：

输入：words = ["omk"]
输出：[]

1
2

示例 3：

输入：words = ["adsdf","sfd"]
输出：["adsdf","sfd"]

1
2

题解:

解题思路：这道题可以使用哈希表来解决。我们可以使用一个字典 keyboard 来记录每个字母所在的行数，然后遍历字符串列表中的每个字符串，对于每个字符串，我们可以将其转换为小写字母，然后判断它的每个字符是否都在同一行。如果是，则将其添加到相应的行中；否则，忽略该字符串。

class Solution:
    def findWords(self, words: List[str]) -> List[str]:
        # 定义行字典,同一行的结果相同
        keyboard = {
            'q': 1, 'w': 1, 'e': 1, 'r': 1, 't': 1, 'y': 1, 'u': 1, 'i': 1, 'o': 1, 'p': 1,
            'a': 2, 's': 2, 'd': 2, 'f': 2, 'g': 2, 'h': 2, 'j': 2, 'k': 2, 'l': 2,
            'z': 3, 'x': 3, 'c': 3, 'v': 3, 'b': 3, 'n': 3, 'm': 3
        }
        res = []
        for word in words:
            # all表示每一项都满足条件
            if all(keyboard[word[0].lower()] == keyboard[char.lower()] for char in word):
                res.append(word)
        return res

1
2
3
4
5
6
7
8
9
10
11
12
13
14

在这个代码中，我们首先定义了一个字典 keyboard，它记录了每个字母所在的行数。然后，我们遍历字符串列表中的每个字符串 word，对于每个字符串，我们使用 all() 函数判断它的每个字符是否都在同一行。如果是，则将其添加到结果列表 res 中。最后，我们返回结果列表。

# 29.相对名次

给你一个长度为 n 的整数数组 score ，其中 score[i] 是第 i 位运动员在比赛中的得分。所有得分都 互不相同 。

运动员将根据得分 决定名次 ，其中名次第 1 的运动员得分最高，名次第 2 的运动员得分第 2 高，依此类推。运动员的名次决定了他们的获奖情况：

名次第 1 的运动员获金牌 "Gold Medal" 。

名次第 2 的运动员获银牌 "Silver Medal" 。

名次第 3 的运动员获铜牌 "Bronze Medal" 。

从名次第 4 到第 n 的运动员，只能获得他们的名次编号（即，名次第 x 的运动员获得编号 "x"）。

使用长度为 n 的数组 answer 返回获奖，其中 answer[i] 是第 i 位运动员的获奖情况。

示例 1：

输入：score = [5,4,3,2,1]
输出：["Gold Medal","Silver Medal","Bronze Medal","4","5"]
解释：名次为 [1st, 2nd, 3rd, 4th, 5th] 。

1
2
3

示例 2：

输入：score = [10,3,8,9,4]
输出：["Gold Medal","5","Bronze Medal","Silver Medal","4"]
解释：名次为 [1st, 5th, 3rd, 2nd, 4th] 。

1
2
3

题解:

class Solution:
    def findRelativeRanks(self, score: List[int]) -> List[str]:
        """
        列表排序,并倒序,使用字典存储起来,再一个一个的去找
        :param score:
        :return:
        """
        res = []
        dict1 = {}
        new_nums = sorted(score, reverse=True)
        for index, num in enumerate(new_nums):
            dict1[num] = index + 1
        for s in score:
            if dict1[s] == 1:
                res.append('Gold Medal')
            elif dict1[s] == 2:
                res.append('Silver Medal')
            elif dict1[s] == 3:
                res.append('Bronze Medal')
            else:
                res.append(str(dict1[s]))
        return res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

# 30.数组拆分

给定长度为 2n 的整数数组 nums ，你的任务是将这些数分成 n 对, 例如 (a1, b1), (a2, b2), ..., (an, bn) ，使得从 1 到 n 的 min(ai, bi) 总和最大。

返回该 最大总和 。

示例 1：

输入：nums = [1,4,3,2]
输出：4
解释：所有可能的分法（忽略元素顺序）为：
1. (1, 4), (2, 3) -> min(1, 4) + min(2, 3) = 1 + 2 = 3
2. (1, 3), (2, 4) -> min(1, 3) + min(2, 4) = 1 + 2 = 3
3. (1, 2), (3, 4) -> min(1, 2) + min(3, 4) = 1 + 3 = 4
所以最大总和为 4

1
2
3
4
5
6
7

示例 2：

输入：nums = [6,2,6,5,1,2]
输出：9
解释：最优的分法为 (2, 1), (2, 5), (6, 6). min(2, 1) + min(2, 5) + min(6, 6) = 1 + 2 + 6 = 9

1
2
3

题解:

排序+指定步长遍历

class Solution:
    def arrayPairSum(self, nums: List[int]) -> int:
        sum = 0
        nums.sort()
        for i in range(0, len(nums), 2):
            sum += nums[i]
        return sum

1
2
3
4
5
6
7

# 31.盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

**说明：**你不能倾斜容器。

示例 1：

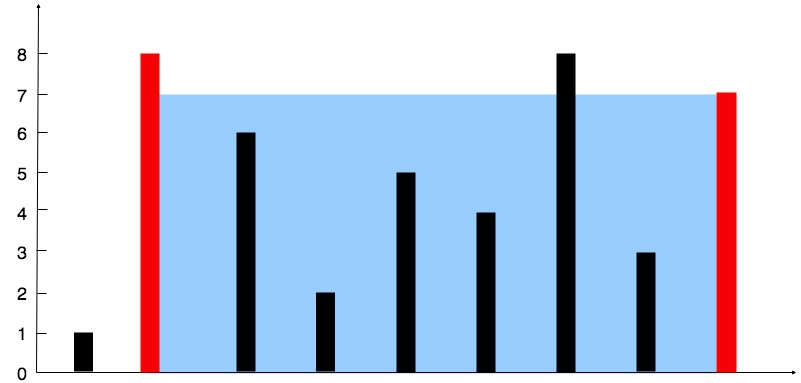
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

1
2
3

示例 2：

输入：height = [1,1]
输出：1

1
2

题解:

class Solution:
    def maxArea(self, height: List[int]) -> int:
        """
        双指针
        :param height:
        :return:
        """
        max_area = 0
        left = 0
        right = len(height) - 1
        while left < right:
            area = (right - left) * min(height[left], height[right])
            max_area = max(max_area, area)
            if height[left] < height[right]:
                left += 1
            else:
                right -= 1
        return max_area

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 32.K 件物品的最大和

袋子中装有一些物品，每个物品上都标记着数字 1 、0 或 -1 。

给你四个非负整数 numOnes 、numZeros 、numNegOnes 和 k 。

袋子最初包含：

numOnes 件标记为 1 的物品。

numZeroes 件标记为 0 的物品。

numNegOnes 件标记为 -1 的物品。

现计划从这些物品中恰好选出 k 件物品。返回所有可行方案中，物品上所标记数字之和的最大值。

示例 1：

输入：numOnes = 3, numZeros = 2, numNegOnes = 0, k = 2
输出：2
解释：袋子中的物品分别标记为 {1, 1, 1, 0, 0} 。取 2 件标记为 1 的物品，得到的数字之和为 2 。
可以证明 2 是所有可行方案中的最大值。

1
2
3
4

示例 2：

输入：numOnes = 3, numZeros = 2, numNegOnes = 0, k = 4
输出：3
解释：袋子中的物品分别标记为 {1, 1, 1, 0, 0} 。取 3 件标记为 1 的物品，1 件标记为 0 的物品，得到的数字之和为 3 。
可以证明 3 是所有可行方案中的最大值。

1
2
3
4

题解:

class Solution:
    def kItemsWithMaximumSum(self, numOnes: int, numZeros: int, numNegOnes: int, k: int) -> int:
        return numOnes - (k - numOnes + numZeros) if k > (numOnes + numZeros) else min(numOnes, k)

1
2
3

class Solution:
    def kItemsWithMaximumSum(self, numOnes: int, numZeros: int, numNegOnes: int, k: int) -> int:
        if k <= numOnes:
            return k
        elif numOnes < k <= (numOnes + numZeros):
            return numOnes
        elif (numOnes + numZeros) < k <= (numOnes + numZeros + numNegOnes):
            return numOnes - (k - numOnes - numZeros)
        else:
            return numOnes - numNegOnes
        return result

1
2
3
4
5
6
7
8
9
10
11

# 33.三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

**注意：**答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

1
2
3
4
5
6
7
8

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

1
2
3

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

1
2
3

题解:

这段代码使用双指针法来解决三数之和问题。首先对数组进行排序，然后遍历数组，将当前数字作为第一个数，使用双指针法找到剩下两个数，使三数之和为 0。在遍历过程中，要注意去除重复的情况。最后返回所有符合条件的三个数的组合

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        nums.sort()
        res = []
        for i in range(len(nums) - 2):
            if nums[i] > 0:
                break
            if i > 0 and nums[i] == nums[i - 1]:
                continue
            left, right = i + 1, len(nums) - 1
            while left < right:
                total = nums[i] + nums[left] + nums[right]
                if total < 0:
                    left += 1
                elif total > 0:
                    right -= 1
                else:
                    res.append([nums[i], nums[left], nums[right]])
                    while left < right and nums[left] == nums[left + 1]:
                        left += 1
                    while left < right and nums[right] == nums[right - 1]:
                        right -= 1
                    left += 1
                    right -= 1
        return res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 34.拆分成最多数目的正偶数之和

给你一个整数 finalSum 。请你将它拆分成若干个 互不相同 的正偶数之和，且拆分出来的正偶数数目最多。

比方说，给你 finalSum = 12 ，那么这些拆分是 符合要求 的（互不相同的正偶数且和为 finalSum）：(2 + 10) ，(2 + 4 + 6) 和 (4 + 8) 。它们中，(2 + 4 + 6) 包含最多数目的整数。注意 finalSum 不能拆分成 (2 + 2 + 4 + 4) ，因为拆分出来的整数必须互不相同。

请你返回一个整数数组，表示将整数拆分成最多数目的正偶数数组。如果没有办法将 finalSum 进行拆分，请你返回一个空数组。你可以按任意顺序返回这些整数。

示例 1：

输入：finalSum = 12
输出：[2,4,6]
解释：以下是一些符合要求的拆分：(2 + 10)，(2 + 4 + 6) 和 (4 + 8) 。
(2 + 4 + 6) 为最多数目的整数，数目为 3 ，所以我们返回 [2,4,6] 。
[2,6,4] ，[6,2,4] 等等也都是可行的解。

1
2
3
4
5

示例 2：

输入：finalSum = 7
输出：[]
解释：没有办法将 finalSum 进行拆分。
所以返回空数组。

1
2
3
4

示例 3：

输入：finalSum = 28
输出：[6,8,2,12]
解释：以下是一些符合要求的拆分：(2 + 26)，(6 + 8 + 2 + 12) 和 (4 + 24) 。
(6 + 8 + 2 + 12) 有最多数目的整数，数目为 4 ，所以我们返回 [6,8,2,12] 。
[10,2,4,12] ，[6,2,4,16] 等等也都是可行的解。

1
2
3
4
5

题解:

class Solution:
    def maximumEvenSplit(self, finalSum: int) -> List[int]:
        """
        怎么样遍历,只需要遍历一次呢?贪心算法 i不断加 finalSum不断减
        :param finalSum:
        :return:
        """
        if finalSum % 2 == 1:
            return []
        res = []
        i = 2
        while i <= finalSum:
            res.append(i)
            finalSum -= i
            i += 2
        # 当i的值大于finalSum时无法继续遍历,需要把剩余的数加到最后一位上
        res[-1] += finalSum
        return res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 35.两数之和 II - 输入有序数组

给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

你所设计的解决方案必须只使用常量级的额外空间。

示例 1：

输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

1
2
3

示例 2：

输入：numbers = [2,3,4], target = 6
输出：[1,3]
解释：2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。

1
2
3

示例 3：

输入：numbers = [-1,0], target = -1
输出：[1,2]
解释：-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

1
2
3

题解:

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        """
        两数之和  使用字典
        :param numbers:
        :param target:
        :return:
        """
        dict1 = {}
        for i, num in enumerate(numbers):
            dict1[num] = i
        for j, num in enumerate(numbers):
            # 先遍历小的
            remain = target - num
            remain_ = dict1.get(remain)
            if remain_ is not None and j < remain_:
                return [j + 1, remain_ + 1]
        return []

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 36.最接近的三数之和

给你一个长度为 n 的整数数组 nums 和一个目标值 target。请你从 nums 中选出三个整数，使它们的和与 target 最接近。

返回这三个数的和。

假定每组输入只存在恰好一个解。

示例 1：

输入：nums = [-1,2,1,-4], target = 1
输出：2
解释：与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。

1
2
3

示例 2：

输入：nums = [0,0,0], target = 1
输出：0

1
2

题解:

class Solution:
    def threeSumClosest(self, nums: List[int], target: int) -> int:
        """
        思路:最关键的是找出最接近的数
        :param nums:
        :param target:
        :return:
        """
        nums.sort()
        ans = nums[0] + nums[1] + nums[2]
        for i in range(len(nums)):
            left = i + 1
            right = len(nums) - 1
            while left < right:
                total = nums[i] + nums[left] + nums[right]
                if abs(target - total) < abs(target - ans):
                    ans = total
                if total > target:
                    right -= 1
                elif total < target:
                    left += 1
                else:
                    return total
        return ans

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# 37.最大子序列交替和

一个下标从 0 开始的数组的 交替和 定义为偶数下标处元素之和减去奇数下标处元素之和。

比方说，数组 [4,2,5,3] 的交替和为 (4 + 5) - (2 + 3) = 4 。

给你一个数组 nums ，请你返回 nums 中任意子序列的 最大交替和 （子序列的下标重新从 0 开始编号）。

一个数组的 子序列 是从原数组中删除一些元素后（也可能一个也不删除）剩余元素不改变顺序组成的数组。比方说，[2,7,4] 是 [4,**2**,3,**7**,2,1,**4**] 的一个子序列（加粗元素），但是 [2,4,2] 不是。

示例 1：

输入：nums = [4,2,5,3]
输出：7
解释：最优子序列为 [4,2,5] ，交替和为 (4 + 5) - 2 = 7 。

1
2
3

示例 2：

输入：nums = [5,6,7,8]
输出：8
解释：最优子序列为 [8] ，交替和为 8 。

1
2
3

示例 3：

输入：nums = [6,2,1,2,4,5]
输出：10
解释：最优子序列为 [6,1,5] ，交替和为 (6 + 5) - 1 = 10 。

1
2
3

题解:

class Solution:
    def maxAlternatingSum(self, nums: List[int]) -> int:
        """
        最大子序列交替和:偶数尽量大,奇数尽量小,且最后一个奇数可以不要
        可以使用贪心算法
        :param nums:
        :return:
        """
        res = nums[0]
        for i in range(1, len(nums)):
            res += max(nums[i] - nums[i - 1], 0)
        return res

1
2
3
4
5
6
7
8
9
10
11
12

# 38.四数之和

给你一个由 n 个整数组成的数组 nums ，和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] （若两个四元组元素一一对应，则认为两个四元组重复）：

0 <= a, b, c, d < n

a、b、c 和 d 互不相同

nums[a] + nums[b] + nums[c] + nums[d] == target

你可以按 任意顺序 返回答案。

示例 1：

输入：nums = [1,0,-1,0,-2,2], target = 0
输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

1
2

示例 2：

输入：nums = [2,2,2,2,2], target = 8
输出：[[2,2,2,2]]

1
2

题解:

class Solution:
    def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
        """
        四数之和 转化为三数之和,理清楚第一个数和第二个之间的关系
        :param nums:
        :param target:
        :return:
        """
        nums.sort()
        res = []
        n = len(nums)
        for i in range(n - 3):
            if i > 0 and nums[i] == nums[i - 1]:
                continue
            for j in range(i + 1, n - 2):
                if j > i + 1 and nums[j] == nums[j - 1]:
                    continue
                left, right = j + 1, n - 1
                while left < right:
                    s = nums[i] + nums[j] + nums[left] + nums[right]
                    if s == target:
                        res.append([nums[i], nums[j], nums[left], nums[right]])
                        while left < right and nums[left] == nums[left + 1]:
                            left += 1
                        while left < right and nums[right] == nums[right - 1]:
                            right -= 1
                        left += 1
                        right -= 1
                    elif s > target:
                        right -= 1
                    else:
                        left += 1
        return res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

# 39.字符串相加

给定两个字符串形式的非负整数 num1 和num2 ，计算它们的和并同样以字符串形式返回。

你不能使用任何內建的用于处理大整数的库（比如 BigInteger），也不能直接将输入的字符串转换为整数形式。

示例 1：

输入：num1 = "11", num2 = "123"
输出："134"

1
2

示例 2：

输入：num1 = "456", num2 = "77"
输出："533"

1
2

示例 3：

输入：num1 = "0", num2 = "0"
输出："0"

1
2

题解:

class Solution:
    def addStrings(self, num1: str, num2: str) -> str:
        """
        双指针
        :param num1:
        :param num2:
        :return:
        """
        res = ""
        i, j, carry = len(num1) - 1, len(num2) - 1, 0
        while i >= 0 or j >= 0:
            n1 = int(num1[i]) if i >= 0 else 0
            n2 = int(num2[j]) if j >= 0 else 0
            all = n1 + n2 + carry
            carry = all // 10
            res = str(all % 10) + res
            i -= 1
            j -= 1
        return "1" + res if carry else res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# 40.模拟行走机器人

机器人在一个无限大小的 XY 网格平面上行走，从点 (0, 0) 处开始出发，面向北方。该机器人可以接收以下三种类型的命令 commands ：

-2 ：向左转 90 度

-1 ：向右转 90 度

1 <= x <= 9 ：向前移动 x 个单位长度

在网格上有一些格子被视为障碍物 obstacles 。第 i 个障碍物位于网格点 obstacles[i] = (xi, yi) 。

机器人无法走到障碍物上，它将会停留在障碍物的前一个网格方块上，但仍然可以继续尝试进行该路线的其余部分。

返回从原点到机器人所有经过的路径点（坐标为整数）的最大欧式距离的平方。（即，如果距离为 5 ，则返回 25 ）

注意：

北表示 +Y 方向。

东表示 +X 方向。

南表示 -Y 方向。

西表示 -X 方向。

示例 1：

输入：commands = [4,-1,3], obstacles = []
输出：25
解释：
机器人开始位于 (0, 0)：
1. 向北移动 4 个单位，到达 (0, 4)
2. 右转
3. 向东移动 3 个单位，到达 (3, 4)
距离原点最远的是 (3, 4) ，距离为 32 + 42 = 25

1
2
3
4
5
6
7
8

示例 2：

输入：commands = [4,-1,4,-2,4], obstacles = [[2,4]]
输出：65
解释：机器人开始位于 (0, 0)：
1. 向北移动 4 个单位，到达 (0, 4)
2. 右转
3. 向东移动 1 个单位，然后被位于 (2, 4) 的障碍物阻挡，机器人停在 (1, 4)
4. 左转
5. 向北走 4 个单位，到达 (1, 8)
距离原点最远的是 (1, 8) ，距离为 12 + 82 = 65

1
2
3
4
5
6
7
8
9

题解:

class Solution:
    def robotSim(self, commands: List[int], obstacles: List[List[int]]) -> int:
        # 转为元组
        obstacles_set = set(map(tuple, obstacles))
        # x和y轴
        x, y = 0, 0
        # 方向 0北 1东 2南 3西
        direction = 0
        # 北 东 南 西的顺序
        direction_for = [[0, 1], [1, 0], [0, -1], [-1, 0]]
        # 结果集
        max_result = 0
        for command in commands:
            # 如果确定direction的方向
            if command == -2:
                direction = (direction + 3) % 4
            elif command == -1:
                direction = (direction + 1) % 4
            else:
                # 每走一步都需要判断是否会遇到障碍物
                for i in range(command):
                    next_x, next_y = x + direction_for[direction][0], y + direction_for[direction][1]
                    if (next_x, next_y) in obstacles_set:
                        break
                    else:
                        # 需要重置x和y的位置
                        x, y = next_x, next_y
                        max_result = max(max_result, next_x ** 2 + next_y ** 2)
        return max_result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

02-链表 →