# 一.堆简介
# 1.什么是堆?
堆(Heap)是一种重要的数据结构,通常用于实现优先队列和一些其他算法。堆具有以下主要特点:
完全二叉树结构: 堆通常是一个完全二叉树,这意味着树中的每个节点都有最多两个子节点,除了最后一层,其他层都是满的。这种特性使得堆可以有效地使用数组来表示,因为数组的索引操作非常高效。
堆序性质: 堆分为两种主要类型,最小堆和最大堆,它们都具有堆序性质。在最小堆中,每个节点的值都小于或等于其子节点的值,根节点的值最小。在最大堆中,每个节点的值都大于或等于其子节点的值,根节点的值最大。
堆的操作: 堆支持一些基本操作,包括插入元素、删除根节点(最小或最大元素)、查找根节点(最小或最大元素),以及堆化操作(将一个无序数组或树转化为堆)。这些操作的时间复杂度通常为 O(log n),其中 n 是堆中元素的数量。
应用: 堆广泛用于解决各种问题,如优先队列(用于任务调度、Dijkstra 算法等)、堆排序算法、求中位数、Top K 问题、图算法(Prim 和 Kruskal 算法中的最小生成树等)等。由于其高效的插入和删除操作,堆在这些问题中表现出色。
实现: 堆可以用数组来表示。在数组中,根节点通常位于索引 0,对于节点 i,其左子节点位于 2i + 1,右子节点位于 2i + 2。这种表示方法使得堆的操作更加高效。堆可以是最小堆或最大堆,具体类型取决于问题需求。
平衡性: 堆是一种自平衡数据结构,即在插入和删除操作后,堆仍然保持堆序性质。这是通过堆化操作来实现的,它可以向上(上滤)或向下(下滤)调整节点的位置,以满足堆的要求。
堆是一种非常有用的数据结构,用于解决许多与优先级相关的问题和算法。最小堆和最大堆的差异在于它们的堆序性质,但它们都具有相似的操作和实现方式。理解堆的基本原理和操作对于编写高效的算法非常重要。
# 2.建堆
- 找到最后一个非叶子节点
- 从后向前,对每个节点执行下潜
一些规律
- 一棵满二叉树节点个数为 $2^h-1$,如下例中高度 $h=3$ 节点数是 $2^3-1=7$
- 非叶子节点范围为 $[0, size/2-1]$
算法时间复杂度分析
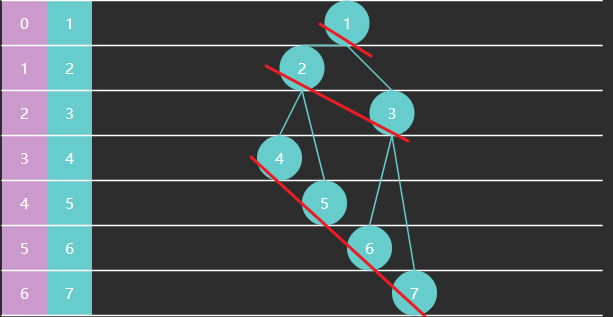
下面看交换次数的推导:设节点高度为 3
| 本层节点数 | 高度 | 下潜最多交换次数(高度-1) | |
|---|---|---|---|
| 4567 这层 | 4 | 1 | 0 |
| 23 这层 | 2 | 2 | 1 |
| 1 这层 | 1 | 3 | 2 |
每一层的交换次数为:$节点个数*此节点交换次数$,总的交换次数为
$$ \begin{aligned} & 4 * 0 + 2 * 1 + 1 * 2 \
& \frac{8}{2}*0 + \frac{8}{4}*1 + \frac{8}{8}*2 \
& \frac{8}{2^1}*0 + \frac{8}{2^2}*1 + \frac{8}{2^3}*2\
\end{aligned} $$
即
$$ \sum_{i=1}^{h}(\frac{2^h}{2^i}*(i-1)) $$
在 https://www.wolframalpha.com/ 输入
Sum[\(40)Divide[Power[2,x],Power[2,i]]*\(40)i-1\(41)\(41),{i,1,x}]
推导出
$$ 2^h -h -1 $$
其中 $2^h \approx n$,$h \approx \log_2{n}$,因此有时间复杂度 $O(n)$
建堆方法:
int[] array;
int size;
// 建堆
private void heapify() {
// 如何找到最后一个非叶子节点 size / 2 - 1,并不断往前遍历
for (int i = size / 2 - 1; i >= 0; i--) {
down(i);
}
}
// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大
private void down(int parent) {
//找到左孩子坐标
int left = parent * 2 + 1;
//找到右孩子坐标
int right = left + 1;
int max = parent;
if (left < size && array[left] > array[max]) {
max = left;
}
if (right < size && array[right] > array[max]) {
max = right;
}
if (max != parent) { // 找到了更大的孩子
swap(max, parent);
down(max);
}
}
// 交换两个索引处的元素
private void swap(int i, int j) {
int t = array[i];
array[i] = array[j];
array[j] = t;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# 3.大顶堆
以大顶堆为例,相对于之前的优先级队列,增加了堆化等方法
- 下潜,表示当前节点和左子结点和右子节点进行交换,并且不断递归
- 父找子 left=parent x 2+1 right=parent x 2+2
- 上浮,标识当前节点和父节点进行交换,并且不断找上面的父节点
- parent=(child-1)/2 找父节点
public class MaxHeap {
int[] array;
int size;
public MaxHeap(int capacity) {
this.array = new int[capacity];
}
/**
* 获取堆顶元素
*
* @return 堆顶元素
*/
public int peek() {
//获取堆顶元素
return array[0];
}
/**
* 删除堆顶元素
*
* @return 堆顶元素
*/
public int poll() {
//获取堆顶元素
int top = array[0];
//交换堆顶和堆底
swap(0, size - 1);
//容量--
size--;
//堆顶下沉
down(0);
return top;
}
/**
* 删除指定索引处元素
*
* @param index 索引
* @return 被删除元素
*/
public int poll(int index) {
int deleted = array[index];
swap(index, size - 1);
size--;
down(index);
return deleted;
}
/**
* 替换堆顶元素
* @param replaced 新元素
*/
public void replace(int replaced) {
array[0] = replaced;
down(0);
}
/**
* 堆的尾部添加元素
*
* @param offered 新元素
* @return 是否添加成功
*/
public boolean offer(int offered) {
if (size == array.length) {
return false;
}
up(offered);
size++;
return true;
}
// 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶
private void up(int offered) {
//默认插入位置在最后的index
int child = size;
while (child > 0) {
//父节点的位置
int parent = (child - 1) / 2;
//上浮
if (offered > array[parent]) {
array[child] = array[parent];
} else {
break;
}
//把父节点的坐标给child
child = parent;
}
//不要忘了赋值
array[child] = offered;
}
public MaxHeap(int[] array) {
this.array = array;
this.size = array.length;
heapify();
}
// 建堆
private void heapify() {
// 如何找到最后一个非叶子节点 size / 2 - 1,并不断往前遍历
for (int i = size / 2 - 1; i >= 0; i--) {
down(i);
}
}
// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大
private void down(int parent) {
//找到左孩子坐标
int left = parent * 2 + 1;
//找到右孩子坐标
int right = left + 1;
int max = parent;
if (left < size && array[left] > array[max]) {
max = left;
}
if (right < size && array[right] > array[max]) {
max = right;
}
if (max != parent) { // 找到了更大的孩子
swap(max, parent);
down(max);
}
}
// 交换两个索引处的元素
private void swap(int i, int j) {
int t = array[i];
array[i] = array[j];
array[j] = t;
}
public static void main(String[] args) {
int[] array = {1, 2, 3, 4, 5, 6, 7};
MaxHeap maxHeap = new MaxHeap(array);
System.out.println(Arrays.toString(maxHeap.array));
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
# 4.关键方法
// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大
private void down(int parent) {
//找到左孩子坐标
int left = parent * 2 + 1;
//找到右孩子坐标
int right = left + 1;
int max = parent;
if (left < size && array[left] > array[max]) {
max = left;
}
if (right < size && array[right] > array[max]) {
max = right;
}
if (max != parent) { // 找到了更大的孩子
swap(max, parent);
down(max);
}
}
// 交换两个索引处的元素
private void swap(int i, int j) {
int t = array[i];
array[i] = array[j];
array[j] = t;
}
// 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶
private void up(int offered) {
//默认插入位置在最后的index
int child = size;
while (child > 0) {
//父节点的位置
int parent = (child - 1) / 2;
//上浮
if (offered > array[parent]) {
array[child] = array[parent];
} else {
break;
}
//把父节点的坐标给child
child = parent;
}
//不要忘了赋值
array[child] = offered;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# 5.小顶堆
public class MinHeap {
int[] array;
int size;
public MinHeap(int capacity) {
this.array = new int[capacity];
}
public boolean isFull() {
return size == array.length;
}
/**
* 获取堆顶元素
*
* @return 堆顶元素
*/
public int peek() {
return array[0];
}
/**
* 删除堆顶元素
*
* @return 堆顶元素
*/
public int poll() {
int top = array[0];
swap(0, size - 1);
size--;
down(0);
return top;
}
/**
* 删除指定索引处元素
*
* @param index 索引
* @return 被删除元素
*/
public int poll(int index) {
int deleted = array[index];
swap(index, size - 1);
size--;
down(index);
return deleted;
}
/**
* 替换堆顶元素
*
* @param replaced 新元素
*/
public void replace(int replaced) {
array[0] = replaced;
down(0);
}
/**
* 堆的尾部添加元素
*
* @param offered 新元素
* @return 是否添加成功
*/
public boolean offer(int offered) {
if (size == array.length) {
return false;
}
up(offered);
size++;
return true;
}
// 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶
private void up(int offered) {
int child = size;
while (child > 0) {
int parent = (child - 1) / 2;
if (offered < array[parent]) {
array[child] = array[parent];
} else {
break;
}
child = parent;
}
array[child] = offered;
}
public MinHeap(int[] array) {
this.array = array;
this.size = array.length;
heapify();
}
// 建堆
private void heapify() {
// 如何找到最后这个非叶子节点 size / 2 - 1
for (int i = size / 2 - 1; i >= 0; i--) {
down(i);
}
}
// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大
private void down(int parent) {
int left = parent * 2 + 1;
int right = left + 1;
int min = parent;
if (left < size && array[left] < array[min]) {
min = left;
}
if (right < size && array[right] < array[min]) {
min = right;
}
if (min != parent) { // 找到了更大的孩子
swap(min, parent);
down(min);
}
}
// 交换两个索引处的元素
private void swap(int i, int j) {
int t = array[i];
array[i] = array[j];
array[j] = t;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
# 6.JDK 的优先队列
// 大顶堆
private PriorityQueue<Integer> left = new PriorityQueue<>( (a, b) -> b-a);
// 默认是小顶堆
private PriorityQueue<Integer> right = new PriorityQueue<>();
2
3
4
# 二.堆题目
# 1.堆排序
算法描述
- heapify 建立大顶堆
- 将堆顶与堆底交换(最大元素被交换到堆底),缩小并下潜调整堆
- 重复第二步直至堆里剩一个元素
可以使用之前课堂例题的大顶堆来实现
int[] array = {1, 2, 3, 4, 5, 6, 7};
MaxHeap maxHeap = new MaxHeap(array);
System.out.println(Arrays.toString(maxHeap.array));
//判断堆的剩余元素个数
while (maxHeap.size > 1) {
//交换堆顶和堆底,把最大的移到堆底
maxHeap.swap(0, maxHeap.size - 1);
//将堆底的元素排除
maxHeap.size--;
//堆顶的元素需要下沉
maxHeap.down(0);
}
System.out.println(Arrays.toString(maxHeap.array));
2
3
4
5
6
7
8
9
10
11
12
13
# 2.数组中第 K 大元素-力扣 215 题
小顶堆(可删去用不到代码)
class MinHeap {
int[] array;
int size;
public MinHeap(int capacity) {
array = new int[capacity];
}
private void heapify() {
for (int i = (size >> 1) - 1; i >= 0; i--) {
down(i);
}
}
public int poll() {
swap(0, size - 1);
size--;
down(0);
return array[size];
}
public int poll(int index) {
swap(index, size - 1);
size--;
down(index);
return array[size];
}
public int peek() {
return array[0];
}
public boolean offer(int offered) {
if (size == array.length) {
return false;
}
up(offered);
size++;
return true;
}
public void replace(int replaced) {
array[0] = replaced;
down(0);
}
private void up(int offered) {
int child = size;
while (child > 0) {
int parent = (child - 1) >> 1;
if (offered < array[parent]) {
array[child] = array[parent];
} else {
break;
}
child = parent;
}
array[child] = offered;
}
private void down(int parent) {
int left = (parent << 1) + 1;
int right = left + 1;
int min = parent;
if (left < size && array[left] < array[min]) {
min = left;
}
if (right < size && array[right] < array[min]) {
min = right;
}
if (min != parent) {
swap(min, parent);
down(min);
}
}
// 交换两个索引处的元素
private void swap(int i, int j) {
int t = array[i];
array[i] = array[j];
array[j] = t;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
题解 1
public int findKthLargest(int[] numbers, int k) {
MinHeap heap = new MinHeap(k);
for (int i = 0; i < k; i++) {
heap.offer(numbers[i]);
}
for (int i = k; i < numbers.length; i++) {
if(numbers[i] > heap.peek()){
heap.replace(numbers[i]);
}
}
return heap.peek();
}
2
3
4
5
6
7
8
9
10
11
12
求数组中的第 K 大元素,使用堆并不是最佳选择,可以采用快速选择算法
题解 2
public int findKthLargest(int[] numbers, int k) {
//小顶堆,先加入2个
PriorityQueue<Integer> queue = new PriorityQueue<>();
for (int i = 0; i < k; i++) {
queue.add(numbers[i]);
}
//再加入后面剩下的
for (int i = k; i < numbers.length; i++) {
if (numbers[i] > queue.peek()) {
queue.poll();
queue.add(numbers[i]);
}
}
return queue.peek();
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 3.数据流中第 K 大元素-力扣 703 题
上题的小顶堆加一个方法
class MinHeap {
// ...
public boolean isFull() {
return size == array.length;
}
}
2
3
4
5
6
题解 1
class KthLargest {
private MinHeap heap;
public KthLargest(int k, int[] nums) {
heap = new MinHeap(k);
for(int i = 0; i < nums.length; i++) {
add(nums[i]);
}
}
public int add(int val) {
if(!heap.isFull()){
heap.offer(val);
} else if(val > heap.peek()){
heap.replace(val);
}
return heap.peek();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
求数据流中的第 K 大元素,使用堆最合适不过
题解 2
private PriorityQueue<Integer> queue;
private int k = 0;
public E03Leetcode703_02(int k, int[] nums) {
this.k = k;
queue = new PriorityQueue();
for (int num : nums) {
add(num);
}
}
// 此方法会被不断调用, 模拟数据流中新来的元素
public int add(int val) {
if (queue.size() < k) {
queue.offer(val);
} else if (queue.peek() < val) {
queue.poll();
queue.offer(val);
}
return queue.peek();
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 4.数据流的中位数-力扣 295 题
可以扩容的 heap, max 用于指定是大顶堆还是小顶堆
public class Heap {
int[] array;
int size;
boolean max;
public int size() {
return size;
}
public Heap(int capacity, boolean max) {
this.array = new int[capacity];
this.max = max;
}
/**
* 获取堆顶元素
*
* @return 堆顶元素
*/
public int peek() {
return array[0];
}
/**
* 删除堆顶元素
*
* @return 堆顶元素
*/
public int poll() {
int top = array[0];
swap(0, size - 1);
size--;
down(0);
return top;
}
/**
* 删除指定索引处元素
*
* @param index 索引
* @return 被删除元素
*/
public int poll(int index) {
int deleted = array[index];
swap(index, size - 1);
size--;
down(index);
return deleted;
}
/**
* 替换堆顶元素
*
* @param replaced 新元素
*/
public void replace(int replaced) {
array[0] = replaced;
down(0);
}
/**
* 堆的尾部添加元素
*
* @param offered 新元素
*/
public void offer(int offered) {
if (size == array.length) {
grow();
}
up(offered);
size++;
}
private void grow() {
int capacity = size + (size >> 1);
int[] newArray = new int[capacity];
System.arraycopy(array, 0,
newArray, 0, size);
array = newArray;
}
// 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶
private void up(int offered) {
int child = size;
while (child > 0) {
int parent = (child - 1) / 2;
boolean cmp = max ? offered > array[parent] : offered < array[parent];
if (cmp) {
array[child] = array[parent];
} else {
break;
}
child = parent;
}
array[child] = offered;
}
public Heap(int[] array, boolean max) {
this.array = array;
this.size = array.length;
this.max = max;
heapify();
}
// 建堆
private void heapify() {
// 如何找到最后这个非叶子节点 size / 2 - 1
for (int i = size / 2 - 1; i >= 0; i--) {
down(i);
}
}
// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大
private void down(int parent) {
int left = parent * 2 + 1;
int right = left + 1;
int min = parent;
if (left < size && (max ? array[left] > array[min] : array[left] < array[min])) {
min = left;
}
if (right < size && (max ? array[right] > array[min] : array[right] < array[min])) {
min = right;
}
if (min != parent) { // 找到了更大的孩子
swap(min, parent);
down(min);
}
}
// 交换两个索引处的元素
private void swap(int i, int j) {
int t = array[i];
array[i] = array[j];
array[j] = t;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
题解 1
private Heap left = new Heap(10, false);
private Heap right = new Heap(10, true);
/**
为了保证两边数据量的平衡
<ul>
<li>两边数据一样时,加入左边</li>
<li>两边数据不一样时,加入右边</li>
</ul>
但是, 随便一个数能直接加入吗?
<ul>
<li>加入左边前, 应该挑右边最小的加入</li>
<li>加入右边前, 应该挑左边最大的加入</li>
</ul>
*/
public void addNum(int num) {
if (left.size() == right.size()) {
right.offer(num);
left.offer(right.poll());
} else {
left.offer(num);
right.offer(left.poll());
}
}
/**
* <ul>
* <li>两边数据一致, 左右各取堆顶元素求平均</li>
* <li>左边多一个, 取左边元素</li>
* </ul>
*/
public double findMedian() {
if (left.size() == right.size()) {
return (left.peek() + right.peek()) / 2.0;
} else {
return left.peek();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
本题还可以使用平衡二叉搜索树求解,不过代码比两个堆复杂
题解 2
/**
* 为了保证两边数据量的平衡
* <ul>
* <li>两边个数一样时,左边个数加一</li>
* <li>两边个数不一样时,右边个数加一</li>
* </ul>
* 但是, 随便一个数能直接加入吗?
* <ul>
* <li>左边个数加一时, 把新元素加在右边,弹出右边最小的加入左边</li>
* <li>右边个数加一时, 把新元素加在左边,弹出左边最小的加入右边</li>
* </ul>
*/
public void addNum(int num) {
if (left.size() == right.size()) {
right.offer(num);
left.offer(right.poll());
} else {
left.offer(num);
right.offer(left.poll());
}
}
/**
* <ul>
* <li>两边数据一致, 左右各取堆顶元素求平均</li>
* <li>左边多一个, 取左边堆顶元素</li>
* </ul>
*/
public double findMedian() {
if (left.size() == right.size()) {
return (left.peek() + right.peek()) / 2.0;
} else {
return left.peek();
}
}
// 大顶堆
private PriorityQueue<Integer> left = new PriorityQueue<>(
(a, b) -> Integer.compare(b, a)
);
// 默认是小顶堆
private PriorityQueue<Integer> right = new PriorityQueue<>();
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
