一.哈夫曼算法

1.什么是编码?

简单说就是建立【字符】到【数字】的对应关系，如下面大家熟知的 ASC II 编码表，例如，可以查表得知字符【a】对应的数字是十六进制数【0x61】

\	00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
0000	00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
0010	10	11	12	13	14	15	16	17	18	19	1a	1b	1c	1d	1e	1f
0020	20	!	"	#	$	%	&	'	(	)	*	+	,	-	.	/
0030	0	1	2	3	4	5	6	7	8	9	:	;	<	=	>	?
0040	@	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O
0050	P	Q	R	S	T	U	V	W	X	Y	Z	[	\	]	^	_
0060	`	a	b	c	d	e	f	g	h	i	j	k	l	m	n	o
0070	p	q	r	s	t	u	v	w	x	y	z	{	|	}	~	7f

注：一些直接以十六进制数字标识的是那些不可打印字符

2.编码传输规则

传输时的编码

• java 中每个 char 对应的数字会占用固定长度 2 个字节
• 如果在传输中仍采用上述规则，传递 abbccccccc 这 10 个字符
  • 实际的字节为 0061006200620063006300630063006300630063（16 进制表示）
  • 总共 20 个字节，不经济

现在希望找到一种最节省字节的传输方式，怎么办？

假设传输的字符中只包含 a，b，c 这 3 个字符，有同学重新设计一张二进制编码表，见下图

• 0 表示 a
• 1 表示 b
• 10 表示 c

现在还是传递 abbccccccc 这 10 个字符

• 实际的字节为 01110101010101010 （二进制表示）
• 总共需要 17 bits，也就是 2 个字节多一点，行不行？

不行，因为解码会出现问题，因为 10 会被错误的解码成 ba，而不是 c

• 解码后结果为 abbbababababababa，是错误的

怎么解决？必须保证编码后的二进制数字，要能区分它们的前缀（prefix-free）

用满二叉树结构编码，可以确保前缀不重复

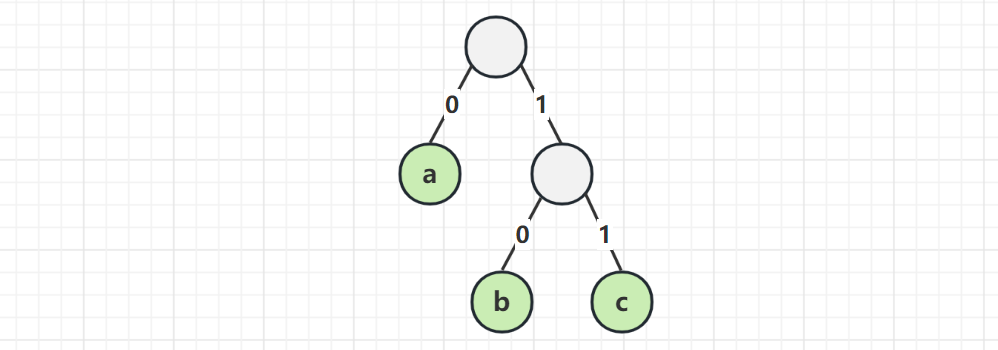
• 向左走 0，向右走 1
• 走到叶子字符，累计起来的 0 和 1 就是该字符的二进制编码

再来试一遍

• a 的编码 0
• b 的编码 10
• c 的编码 11

现在还是传递 abbccccccc 这 10 个字符

• 实际的字节为 0101011111111111111（二进制表示）
• 总共需要 19 bits，也是 2 个字节多一点，并且解码没有问题了，行不行？

这回解码没问题了，但并非最少字节，因为 c 的出现频率高（7 次）a 的出现频率低（1 次），因此出现频率高的字符编码成短数字更经济

3.Huffman 编码

考察下面的树

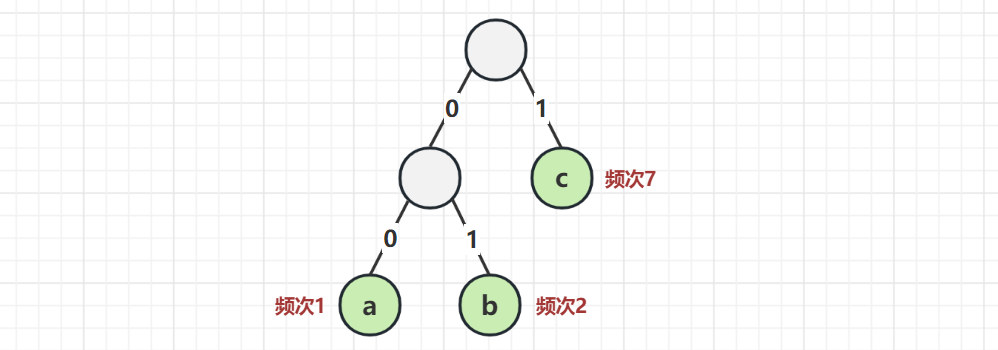
• 00 表示 a
• 01 表示 b
• 1 表示 c

现在还是传递 abbccccccc 这 10 个字符

• 实际的字节为 000101 1111111 （二进制表示）
• 总共需要 13 bits，这棵树就称之为 Huffman 树
• 根据 Huffman 树对字符和数字进行编解码，就是 Huffman 编解码

二.哈夫曼树

1.什么 Huffman 树?

哈夫曼树，英文名 huffman tree,它是一种的叶子节点带有权重的特殊二叉树，也叫最优二叉树。

哈夫曼(Huffman)编码是上个世纪五十年代由哈夫曼教授研制开发的，它借助了数据结构当中的树型结构，在哈夫曼算法的支持下构造出一棵最优二叉树，我们把这类树命名为哈夫曼树。

哈夫曼树是带权路径长度最短的树，权值较大的节点离根较近。

2.哈夫曼树特点

哈夫曼树的特点：

• 没有度为1的节点（每个非叶子节点都是由两个最小值的节点构成）

• n 个叶子节点的哈夫曼树总共有2n-1个节点;

• 哈夫曼树的任意非叶节点的左右子树交换后仍是哈夫曼树；

• 对同一组权值{w1，w2，…}，存在不同构的两个哈夫曼树，但是它们的总权值相等。

• 形成了这样的一颗哈夫曼树，这也是二叉树的前序

3.节点总数证明

证明哈夫曼树中有 n 个叶子节点的树总共有 2n-1 个节点可以使用数学归纳法。以下是证明的步骤：

步骤 1：基础情况 当 n=1 时，只有一个叶子节点，因此整棵哈夫曼树只有一个节点。这是一个基础情况。

步骤 2：归纳假设 假设对于某个正整数 k，当哈夫曼树有 k 个叶子节点时，它总共有 2k-1 个节点。

步骤 3：归纳证明 现在，考虑有 k+1 个叶子节点的情况。我们可以将这个问题分成两个部分：

部分 1： 从 k 个叶子节点构建一个哈夫曼树，根据归纳假设，这个树有 2k-1 个节点。

部分 2： 现在，我们添加一个额外的叶子节点，构建一个新的哈夫曼树。在这个新树中，我们需要添加一个新的内部节点，作为新叶子节点和部分 1 中的树的根节点的父节点。这个新树总共有 2k 个叶子节点和 1 个额外的内部节点，所以共有 2k+1 个节点。

现在，将部分 1 和部分 2 合并在一起，我们得到了有 k+1 个叶子节点的哈夫曼树，总共有(2k-1) + (2k+1) = 2k-1 + 2k+1 = 2(k-1+2) = 2k+1-1 个节点。

这证明了对于 k+1 个叶子节点的情况，有 2k+1-1 个节点，即当 n=k+1 时，也成立。

由于基础情况成立，并且我们已经证明了当 n=k+1 时成立，所以根据数学归纳法，对于所有正整数 n，有 n 个叶子节点的哈夫曼树总共有 2n-1 个节点。

4.Huffman 树特点

哈夫曼树（Huffman Tree）是一种用于数据压缩的树形数据结构，它具有以下几个特点：

1. 最优编码：哈夫曼树被设计用来实现最优的数据压缩编码，这意味着它可以生成具有最小平均编码长度的编码方案，以便在数据传输或存储时能够节省空间。

2. 基于频率：哈夫曼树的构建是基于数据中各个字符（或符号）的出现频率来进行的。频率高的字符被赋予较短的编码，而频率低的字符被赋予较长的编码。

3. 唯一性：对于给定的数据集，存在唯一的哈夫曼树。这意味着如果两个人使用相同的数据集和相同的构建规则来创建哈夫曼树，它们将得到相同的树结构和编码。

4. 前缀编码：哈夫曼编码是一种前缀编码，意味着没有一个字符的编码是另一个字符编码的前缀。这个特性确保在解码时不会产生歧义。

5. 树形结构：哈夫曼树是一种二叉树，它由内部节点和叶子节点组成。叶子节点对应于数据集中的字符，而内部节点是用于构建编码的辅助节点。

6. 压缩率：哈夫曼编码通常能够实现较高的压缩率，尤其是对于具有不同频率分布的数据集。频率高的字符使用较短的编码，从而实现更好的压缩效果。

7. 动态性：哈夫曼编码可以动态地根据数据集的特性进行调整，以适应不同的数据。这使得它在各种应用中都具有灵活性。

总之，哈夫曼树是一种用于数据压缩的有效工具，其特点包括最优编码、基于频率、唯一性、前缀编码、树形结构、高压缩率和动态性。通过合理构建哈夫曼树，可以实现高效的数据压缩和解压缩操作。

三.常见方法

1.内部 Node 节点

/**
 * Node代表字符节点
 */
static class Node {
    /**
     * 字符
     */
    Character ch;
    /**
     * 频次
     */
    int freq;
    /**
     * 左子节点
     */
    Node left;
    /**
     * 右子节点
     */
    Node right;
    /**
     * 编码
     */
    String code;

    public Node(Character ch) {
        this.ch = ch;
    }

    public Node(int freq, Node left, Node right) {
        this.freq = freq;
        this.left = left;
        this.right = right;
    }

    int freq() {
        return freq;
    }

    boolean isLeaf() {
        return left == null;
    }

    @Override
    public String toString() {
        return "Node{" + "ch=" + ch + ", freq=" + freq + '}';
    }
}

2.构造方法

public HuffmanTree(String str) {
    this.str = str;
    // 功能1：统计字符的频率
    char[] chars = str.toCharArray();
    for (char c : chars) {
        Node node = map.computeIfAbsent(c, Node::new);
        node.freq++;
    }
    // 功能2: 构造树
    PriorityQueue<Node> queue = new PriorityQueue<>(Comparator.comparingInt(Node::freq));
    queue.addAll(map.values());
    while (queue.size() >= 2) {
        Node x = queue.poll();
        Node y = queue.poll();
        int freq = x.freq + y.freq;
        queue.offer(new Node(freq, x, y));
    }
    root = queue.poll();
    // 功能3：计算每个字符的编码,
    int sum = dfs(root, new StringBuilder());
    for (Node node : map.values()) {
        System.out.println(node + " " + node.code);
    }
    // 功能4：字符串编码后占用 bits
    System.out.println("总共会占用 bits:" + sum);
}

private int dfs(Node node, StringBuilder code) {
        int sum = 0;
        if (node.isLeaf()) {
            node.code = code.toString();
            sum = node.freq * code.length();
        } else {
            sum += dfs(node.left, code.append("0"));
            sum += dfs(node.right, code.append("1"));
        }
        if (code.length() > 0) {
            code.deleteCharAt(code.length() - 1);
        }
        return sum;
    }

3.编码

public String encode() {
    //abbccccccc
    char[] chars = str.toCharArray();
    StringBuilder sb = new StringBuilder();
    for (char c : chars) {
        sb.append(map.get(c).code);
    }
    return sb.toString();
}

4.解码

public String decode(String str) {
    /*
        从根节点，寻找数字对应的字符
            数字是 0 向左走
            数字是 1 向右走
            如果没走到头，每走一步数字的索引 i++
        走到头就可以找到解码字符，再将 node 重置为根节点
        a 00
        b 10
        c 1
                        i
        0   0   0   1   0   1   1   1   1   1   1   1   1
     */
    char[] chars = str.toCharArray();
    int i = 0;
    StringBuilder sb = new StringBuilder();
    Node node = root;
    //             i = 13  node=root
    // 0001011111111
    while (i < chars.length) {
        if (!node.isLeaf()) { // 非叶子
            if (chars[i] == '0') { // 向左走
                node = node.left;
            } else if (chars[i] == '1') { // 向右走
                node = node.right;
            }
            i++;
        }
        if (node.isLeaf()) {
            sb.append(node.ch);
            node = root;
        }
    }
    return sb.toString();
}

5.完整代码

/**
 * Huffman 树的构建过程
 * 1. 将统计了出现频率的字符，放入优先级队列
 * 2. 每次出队两个频次最低的元素，给它俩找个爹
 * 3. 把爹重新放入队列，重复 2~3
 * 4. 当队列只剩一个元素时，Huffman 树构建完成
 *
 * @author : qinyingjie
 * @date : 2023/9/26
 */
public class HuffmanTree {
    /**
     * Node代表字符节点
     */
    static class Node {
        /**
         * 字符
         */
        Character ch;
        /**
         * 频次
         */
        int freq;
        /**
         * 左子节点
         */
        Node left;
        /**
         * 右子节点
         */
        Node right;
        /**
         * 编码
         */
        String code;

        public Node(Character ch) {
            this.ch = ch;
        }

        public Node(int freq, Node left, Node right) {
            this.freq = freq;
            this.left = left;
            this.right = right;
        }

        int freq() {
            return freq;
        }

        boolean isLeaf() {
            return left == null;
        }

        @Override
        public String toString() {
            return "Node{" + "ch=" + ch + ", freq=" + freq + '}';
        }
    }

    String str;
    /**
     * 统计字符数量,key是字符,value是节点
     */
    Map<Character, Node> map = new HashMap<>();
    /**
     * 根节点
     */
    Node root;

    public HuffmanTree(String str) {
        this.str = str;
        // 功能1：统计字符的频率
        char[] chars = str.toCharArray();
        for (char c : chars) {
            Node node = map.computeIfAbsent(c, Node::new);
            node.freq++;
        }
        // 功能2: 构造树
        PriorityQueue<Node> queue = new PriorityQueue<>(Comparator.comparingInt(Node::freq));
        queue.addAll(map.values());
        while (queue.size() >= 2) {
            Node x = queue.poll();
            Node y = queue.poll();
            int freq = x.freq + y.freq;
            queue.offer(new Node(freq, x, y));
        }
        root = queue.poll();
        // 功能3：计算每个字符的编码,
        int sum = dfs(root, new StringBuilder());
        for (Node node : map.values()) {
            System.out.println(node + " " + node.code);
        }
        // 功能4：字符串编码后占用 bits
        System.out.println("总共会占用 bits:" + sum);
    }

    private int dfs(Node node, StringBuilder code) {
        int sum = 0;
        if (node.isLeaf()) {
            node.code = code.toString();
            sum = node.freq * code.length();
        } else {
            sum += dfs(node.left, code.append("0"));
            sum += dfs(node.right, code.append("1"));
        }
        if (code.length() > 0) {
            code.deleteCharAt(code.length() - 1);
        }
        return sum;
    }

    // 编码
    public String encode() {
        //abbccccccc
        char[] chars = str.toCharArray();
        StringBuilder sb = new StringBuilder();
        for (char c : chars) {
            sb.append(map.get(c).code);
        }
        return sb.toString();
    }

    // 解码
    public String decode(String str) {
        /*
            从根节点，寻找数字对应的字符
                数字是 0 向左走
                数字是 1 向右走
                如果没走到头，每走一步数字的索引 i++
            走到头就可以找到解码字符，再将 node 重置为根节点
            a 00
            b 10
            c 1
                            i
            0   0   0   1   0   1   1   1   1   1   1   1   1
         */
        char[] chars = str.toCharArray();
        int i = 0;
        StringBuilder sb = new StringBuilder();
        Node node = root;
        //             i = 13  node=root
        // 0001011111111
        while (i < chars.length) {
            if (!node.isLeaf()) { // 非叶子
                if (chars[i] == '0') { // 向左走
                    node = node.left;
                } else if (chars[i] == '1') { // 向右走
                    node = node.right;
                }
                i++;
            }
            if (node.isLeaf()) {
                sb.append(node.ch);
                node = root;
            }
        }
        return sb.toString();
    }

    public static void main(String[] args) {
        HuffmanTree tree = new HuffmanTree("abbccccccc");
        String encoded = tree.encode();
        System.out.println(encoded);
        System.out.println(tree.decode(encoded));
    }
}

四.练习题

1.连接棒材的最低费用-力扣 1167 题

题目编号	题目标题	算法思路
1167（Plus 题目）	连接棒材的最低费用	Huffman 树、贪心

为了装修新房，你需要加工一些长度为正整数的棒材 sticks。

如果要将长度分别为 X 和 Y 的两根棒材连接在一起，你需要支付 X + Y 的费用。

由于施工需要，你必须将所有棒材连接成一根。

返回你把所有棒材 sticks 连成一根所需要的最低费用。注意你可以任意选择棒材连接的顺序。

示例 1：
输入：sticks = [2,4,3]
输出：14
解释：先将 2 和 3 连接成 5，花费 5；再将 5 和 4 连接成 9；总花费为 14。

示例 2：
输入：sticks = [1,8,3,5]
输出：30

提示：
1 <= sticks.length <= 10^4
1 <= sticks[i] <= 10^4

题解

/**
 * <h3>连接棒材的最低费用</h3>
 * <p>为了装修新房，你需要加工一些长度为正整数的棒材。如果要将长度分别为 X 和 Y 的两根棒材连接在一起，你需要支付 X + Y 的费用。 返回讲所有棒材连成一根所需要的最低费用。</p>
 */
public class Leetcode1167 {
    /*
        举例 棒材为 [1,8,3,5]

        如果以如下顺序连接(非最优)
        - 1+8=9
        - 9+3=12
        - 12+5=17
        总费用为 9+12+17=38

        如果以如下顺序连接(最优)
        - 1+3=4
        - 4+5=9
        - 8+9=17
        总费用为 4+9+17=30
     */
    int connectSticks(int[] sticks) {
        PriorityQueue<Integer> queue = new PriorityQueue<>();
        for (int stick : sticks) {
            queue.offer(stick);
        }

        int sum = 0;
        while (queue.size() >= 2) {
            Integer x = queue.poll();
            Integer y = queue.poll();
            int c = x + y;
            sum += c;
            queue.offer(c);
        }
        return sum;
    }

    public static void main(String[] args) {
        Leetcode1167 leetcode = new Leetcode1167();
        System.out.println(leetcode.connectSticks(new int[]{1, 8, 3, 5})); // 30
        System.out.println(leetcode.connectSticks(new int[]{2, 4, 3})); // 14
    }
}