一.二叉树简介

1.什么是二叉树?

二叉树是一种常见的树状数据结构，它由节点组成，每个节点最多有两个子节点，分别称为左子节点和右子节点。每个节点包含一个值或数据项，这些节点通过边（通常称为链接或指针）相互连接起来，形成一个层次结构。

2.二叉树的性质?

二叉树的特点包括：

• 根节点：二叉树的顶部节点称为根节点，它是树的起始点，没有父节点。

• 子节点：每个节点可以有零个、一个或两个子节点，分别是左子节点和右子节点。

• 叶节点：没有子节点的节点称为叶节点，它们位于树的末端。

• 高度：树的高度是从根节点到最深叶节点的最长路径的长度。

• 深度：节点的深度是从根节点到该节点的路径长度。

3.二叉树的种类

二叉树有多种不同的种类，它们在树的结构和性质上具有不同的特点。以下是一些常见的二叉树种类：

1. 二叉搜索树（Binary Search Tree，BST）：BST 是一种二叉树，其中每个节点的左子树包含的值都小于该节点的值，右子树包含的值都大于该节点的值。BST 的特性使得它非常适合用于搜索和排序操作。

2. 平衡二叉树（Balanced Binary Tree）：平衡二叉树是一种二叉搜索树，它确保树的高度平衡，从而保持搜索、插入和删除操作的平均时间复杂度为 O(log n)。

3. 完全二叉树（Complete Binary Tree）：

   • 完全二叉树是一种二叉树，除了最后一层，所有层都是完全填充的，而且最后一层的节点从左到右填充，不留空缺。这种树在堆数据结构中常常用于实现。

   • 完全二叉树的特点：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。需要注意的是，满二叉树肯定是完全二叉树，而完全二叉树不一定是满二叉树。

4. 满二叉树（Full Binary Tree）：满二叉树是一种二叉树，每个节点要么没有子节点，要么有两个子节点。所有叶子节点都在同一层上。

5. 完美二叉树（Perfect Binary Tree）：完美二叉树是一种满二叉树，它的所有叶子节点都在同一层，并且每个非叶子节点都有两个子节点。

6. 二叉堆（Binary Heap）：二叉堆是一种特殊的完全二叉树，分为最小堆和最大堆。在最小堆中，每个节点的值都小于或等于其子节点的值；在最大堆中，每个节点的值都大于或等于其子节点的值。堆通常用于实现优先队列等数据结构。

7. 线索二叉树（Threaded Binary Tree）：线索二叉树是一种特殊的二叉树，其中节点的指针指向其前驱和后继节点，这样可以实现更高效的中序遍历。

8. AVL 树：AVL 树是一种自平衡的二叉搜索树，确保树的高度平衡，从而保持插入和删除操作的时间复杂度为 O(log n)。

9. 哈夫曼树（Huffman Tree）: 是用于构建哈夫曼编码的二叉树结构。它是哈夫曼编码算法的核心部分，用于为不同字符分配唯一的二进制编码，以便进行数据压缩。

这些是二叉树的一些常见种类，每种类型都具有不同的特性，适用于不同的应用场景和问题。根据具体需求，选择合适的二叉树类型可以提高算法和数据结构的效率。

4.什么是哈夫曼树

哈夫曼树（Huffman Tree）是用于构建哈夫曼编码的二叉树结构。它是哈夫曼编码算法的核心部分，用于为不同字符分配唯一的二进制编码，以便进行数据压缩。

哈夫曼树的特点如下：

1. 最优性：哈夫曼树是一种最优的二叉树，它能够确保在给定字符的出现频率情况下，编码树的路径长度最短。这意味着使用哈夫曼树生成的哈夫曼编码是具有最小平均编码长度的。

2. 前缀编码：哈夫曼树中没有一个字符的编码是另一个字符编码的前缀。这就是所谓的前缀编码，它确保了在解码时不会出现歧义，因为任何编码序列不会匹配另一个编码的前缀。

3. 频率相关：哈夫曼树的构建是基于字符的出现频率的，出现频率高的字符位于树的较浅位置，而出现频率低的字符位于树的较深位置。

哈夫曼树的构建过程通常涉及以下步骤：

1. 统计字符频率：首先，需要统计输入数据中每个字符的出现频率。

2. 创建叶子节点：为每个字符创建一个叶子节点，将频率作为叶子节点的权重。

3. 构建哈夫曼树：反复合并权重最小的两个节点（可以是叶子节点或内部节点）来构建树，直到只剩下一个根节点为止。合并的过程中，新节点的权重是合并节点的权重之和。

4. 分配编码：从根节点开始，根据路径向左走为 0，向右走为 1，为每个字符分配唯一的编码。编码是从根节点到叶子节点的路径上的二进制序列。

5. 完成哈夫曼树：最终，构建得到的树就是哈夫曼树，其中每个字符都有一个唯一的编码。

哈夫曼树和相应的哈夫曼编码在数据压缩领域得到广泛应用，能够有效地减小数据的存储空间或传输带宽需求，同时保持数据的完整性。

定义:

Huffman Tree，中文名是哈夫曼树或霍夫曼树，它是最优二叉树。

定义：给定 n 个权值作为 n 个叶子结点，构造一棵二叉树，若树的带权路径长度达到最小，则这棵树被称为哈夫曼树。 这个定义里面涉及到了几个陌生的概念，下面就是一颗哈夫曼树，我们来看图解答。

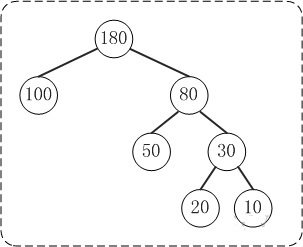
(1) 路径和路径长度

定义：在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为 1，则从根结点到第 L 层结点的路径长度为 L-1。 例子：100 和 80 的路径长度是 1，50 和 30 的路径长度是 2，20 和 10 的路径长度是 3。

(2) 结点的权及带权路径长度

定义：若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。 例子：节点 20 的路径长度是 3，它的带权路径长度= 路径长度 _ 权 = 3 _ 20 = 60。

(3) 树的带权路径长度

定义：树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为 WPL。 例子：示例中，树的 WPL= 1x100 + 2x50 + 3x20 + 3x10 = 100 + 100 + 60 + 30 = 290。

5.父子节点存储

存储规则分为两点:

• 定义树节点与左、右孩子引用（TreeNode）

• 使用数组，前面讲堆时用过，若以 0 作为树的根，索引可以通过如下方式计算

  • 父 = floor((子 - 1) / 2)

  • 左孩子 = 父 * 2 + 1

  • 右孩子 = 父 * 2 + 2

二.二叉树的遍历

1.二叉树遍历方式

遍历也分为两种

1. 广度优先遍历（Breadth-first order）：尽可能先访问距离根最近的节点，也称为层序遍历
2. 深度优先遍历（Depth-first order）：对于二叉树，可以进一步分成三种（要深入到叶子节点）
   1. pre-order 前序遍历，对于每一棵子树，先访问该节点，然后是左子树，最后是右子树
   2. in-order 中序遍历，对于每一棵子树，先访问左子树，然后是该节点，最后是右子树
   3. post-order 后序遍历，对于每一棵子树，先访问左子树，然后是右子树，最后是该节点

2.广度优先

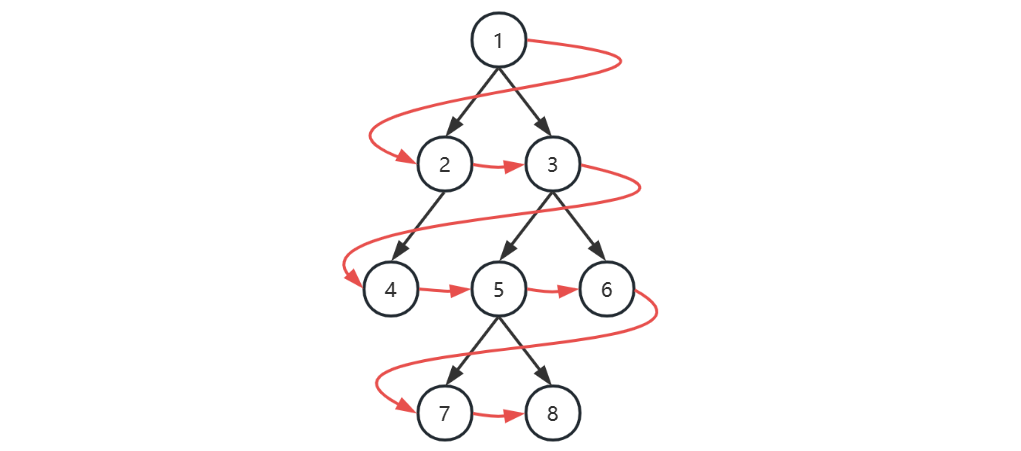
本轮开始时队列	本轮访问节点
[1]	1
[2, 3]	2
[3, 4]	3
[4, 5, 6]	4
[5, 6]	5
[6, 7, 8]	6
[7, 8]	7
[8]	8
[]

1. 初始化，将根节点加入队列
2. 循环处理队列中每个节点，直至队列为空
3. 每次循环内处理节点后，将它的孩子节点（即下一层的节点）加入队列

注意

• 以上用队列来层序遍历是针对 TreeNode 这种方式表示的二叉树

• 对于数组表现的二叉树，则直接遍历数组即可，自然为层序遍历的顺序

3.深度优先

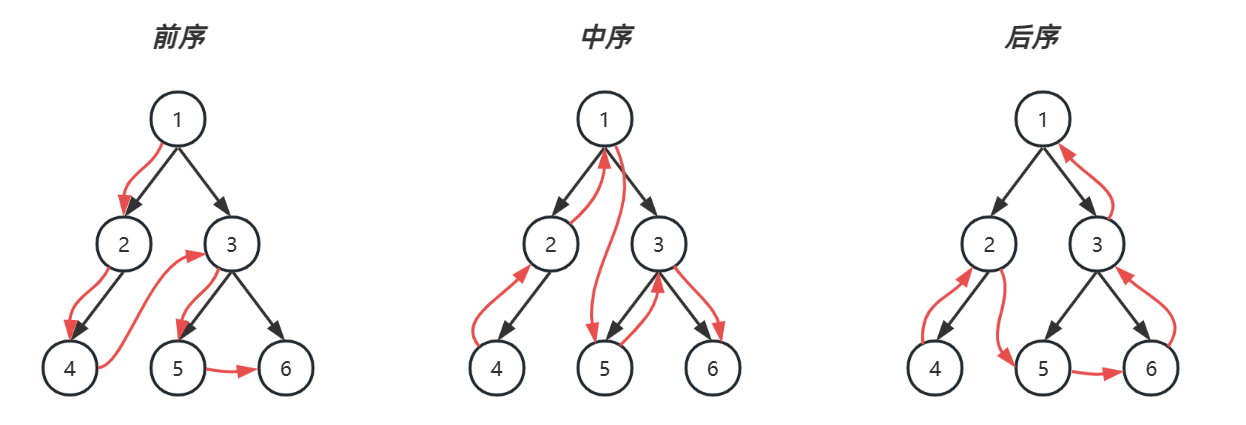
栈暂存	已处理	前序遍历	中序遍历
[1]	1 ✔️ 左 💤 右 💤	1
[1, 2]	2✔️ 左 💤 右 💤 1✔️ 左 💤 右 💤	2
[1, 2, 4]	4✔️ 左 ✔️ 右 ✔️ 2✔️ 左 💤 右 💤 1✔️ 左 💤 右 💤	4	4
[1, 2]	2✔️ 左 ✔️ 右 ✔️ 1✔️ 左 💤 右 💤		2
[1]	1✔️ 左 ✔️ 右 💤		1
[1, 3]	3✔️ 左 💤 右 💤 1✔️ 左 ✔️ 右 💤	3
[1, 3, 5]	5✔️ 左 ✔️ 右 ✔️ 3✔️ 左 💤 右 💤 1✔️ 左 ✔️ 右 💤	5	5
[1, 3]	3✔️ 左 ✔️ 右 💤 1✔️ 左 ✔️ 右 💤		3
[1, 3, 6]	6✔️ 左 ✔️ 右 ✔️ 3✔️ 左 ✔️ 右 💤 1✔️ 左 ✔️ 右 💤	6	6
[1, 3]	3✔️ 左 ✔️ 右 ✔️ 1✔️ 左 ✔️ 右 💤
[1]	1✔️ 左 ✔️ 右 ✔️
[]

4.递归实现

/**
 * <h3>前序遍历</h3>
 * @param node 节点
 */
static void preOrder(TreeNode node) {
    if (node == null) {
        return;
    }
    System.out.print(node.val + "\t"); // 值
    preOrder(node.left); // 左
    preOrder(node.right); // 右
}

/**
 * <h3>中序遍历</h3>
 * @param node 节点
 */
static void inOrder(TreeNode node) {
    if (node == null) {
        return;
    }
    inOrder(node.left); // 左
    System.out.print(node.val + "\t"); // 值
    inOrder(node.right); // 右
}

/**
 * <h3>后序遍历</h3>
 * @param node 节点
 */
static void postOrder(TreeNode node) {
    if (node == null) {
        return;
    }
    postOrder(node.left); // 左
    postOrder(node.right); // 右
    System.out.print(node.val + "\t"); // 值
}

5.非递归实现

前序遍历

LinkedListStack<TreeNode> stack = new LinkedListStack<>();
TreeNode curr = root;

while (!stack.isEmpty() || curr != null) {
    if (curr != null) {
        stack.push(curr);
        System.out.println(curr);
        curr = curr.left;
    } else {
        TreeNode pop = stack.pop();
        curr = pop.right;
    }

}

中序遍历

LinkedListStack<TreeNode> stack = new LinkedListStack<>();
TreeNode curr = root;

while (!stack.isEmpty() || curr != null) {
    if (curr != null) {
        stack.push(curr);
        curr = curr.left;
    } else {
        TreeNode pop = stack.pop();
        System.out.println(pop);
        curr = pop.right;
    }
}

后序遍历

LinkedListStack<TreeNode> stack = new LinkedListStack<>();
TreeNode curr = root;
TreeNode pop = null;

while (!stack.isEmpty() || curr != null) {
    if (curr != null) {
        stack.push(curr);
        curr = curr.left;
    } else {
        TreeNode peek = stack.peek();
        if (peek.right == null || peek.right == pop) {
            pop = stack.pop();
            System.out.println(pop);
        } else {
            curr = peek.right;
        }
    }
}

对于后序遍历，向回走时，需要处理完右子树才能 pop 出栈。如何知道右子树处理完成呢？

• 如果栈顶元素的 $right \equiv null$ 表示没啥可处理的，可以出栈

• 如果栈顶元素的 $right \neq null$，

  • 那么使用 lastPop 记录最近出栈的节点，即表示从这个节点向回走
  • 如果栈顶元素的 $right==lastPop$ 此时应当出栈

对于前、中两种遍历，实际以上代码从右子树向回走时，并未走完全程（stack 提前出栈了）后序遍历以上代码是走完全程了

6.统一写法

下面是一种统一的写法，依据后序遍历修改

LinkedList<TreeNode> stack = new LinkedList<>();

TreeNode curr = root; // 代表当前节点
TreeNode pop = null; // 最近一次弹栈的元素
while (curr != null || !stack.isEmpty()) {
    if (curr != null) {
        colorPrintln("前: " + curr.val, 31);
        stack.push(curr); // 压入栈，为了记住回来的路
        curr = curr.left;
    } else {
        TreeNode peek = stack.peek();
        // 右子树可以不处理, 对中序来说, 要在右子树处理之前打印
        if (peek.right == null) {
            colorPrintln("中: " + peek.val, 36);
            pop = stack.pop();
            colorPrintln("后: " + pop.val, 34);
        }
        // 右子树处理完成, 对中序来说, 无需打印
        else if (peek.right == pop) {
            pop = stack.pop();
            colorPrintln("后: " + pop.val, 34);
        }
        // 右子树待处理, 对中序来说, 要在右子树处理之前打印
        else {
            colorPrintln("中: " + peek.val, 36);
            curr = peek.right;
        }
    }
}

public static void colorPrintln(String origin, int color) {
    System.out.printf("\033[%dm%s\033[0m%n", color, origin);
}

三.二叉树题目

1.对称二叉树-力扣 101 题

public boolean isSymmetric(TreeNode root) {
    return check(root.left, root.right);
}

public boolean check(TreeNode left, TreeNode right) {
    // 若同时为 null
    if (left == null && right == null) {
        return true;
    }
    // 若有一个为 null (有上一轮筛选，另一个肯定不为 null)
    if (left == null || right == null) {
        return false;
    }
    if (left.val != right.val) {
        return false;
    }
    return check(left.left, right.right) && check(left.right, right.left);
}

类似题目：Leetcode 100 题 - 相同的树

2.二叉树最大深度-力扣 104 题

后序遍历求解

/*
    思路：
    1. 得到左子树深度, 得到右子树深度, 二者最大者加一, 就是本节点深度
    2. 因为需要先得到左右子树深度, 很显然是后序遍历典型应用
    3. 关于深度的定义：从根出发, 离根最远的节点总边数,
        注意: 力扣里的深度定义要多一

        深度2         深度3         深度1
        1            1            1
       / \          / \
      2   3        2   3
                        \
                         4
 */
public int maxDepth(TreeNode node) {
    if (node == null) {
        return 0; // 非力扣题目改为返回 -1
    }
    int d1 = maxDepth(node.left);
    int d2 = maxDepth(node.right);
    return Integer.max(d1, d2) + 1;
}

后序遍历求解-非递归

/*
    思路：
    1. 使用非递归后序遍历, 栈的最大高度即为最大深度
 */
public int maxDepth(TreeNode root) {
    TreeNode curr = root;
    LinkedList<TreeNode> stack = new LinkedList<>();
    int max = 0;
    TreeNode pop = null;
    while (curr != null || !stack.isEmpty()) {
        if (curr != null) {
            stack.push(curr);
            int size = stack.size();
            if (size > max) {
                max = size;
            }
            curr = curr.left;
        } else {
            TreeNode peek = stack.peek();
            if(peek.right == null || peek.right == pop) {
                pop = stack.pop();
            } else {
                curr = peek.right;
            }
        }
    }
    return max;
}

层序遍历求解

/*
    思路：
    1. 使用层序遍历, 层数即最大深度
 */
public int maxDepth(TreeNode root) {
    if(root == null) {
        return 0;
    }
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    int level = 0;
    while (!queue.isEmpty()) {
        level++;
        int size = queue.size();
        for (int i = 0; i < size; i++) {
            TreeNode node = queue.poll();
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
    }
    return level;
}

3.二叉树最小深度-力扣 111 题

后序遍历求解

public int minDepth(TreeNode node) {
    if (node == null) {
        return 0;
    }
    int d1 = minDepth(node.left);
    int d2 = minDepth(node.right);
    if (d1 == 0 || d2 == 0) {
        return d1 + d2 + 1;
    }
    return Integer.min(d1, d2) + 1;
}

相较于求最大深度，应当考虑：

• 当右子树为 null，应当返回左子树深度加一
• 当左子树为 null，应当返回右子树深度加一

上面两种情况满足时，不应该再把为 null 子树的深度 0 参与最小值比较，例如这样

    1
   /
  2

• 正确深度为 2，若把为 null 的右子树的深度 0 考虑进来，会得到错误结果 1

    1
     \
      3
       \
        4

• 正确深度为 3，若把为 null 的左子树的深度 0 考虑进来，会得到错误结果 1

层序遍历求解

遇到的第一个叶子节点所在层就是最小深度

例如，下面的树遇到的第一个叶子节点 3 所在的层就是最小深度，其他 4，7 等叶子节点深度更深，也更晚遇到

     1
    / \
   2   3
  / \
 4   5
    /
   7

代码

public int minDepth(TreeNode root) {
    if(root == null) {
        return 0;
    }
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    int level = 0;
    while (!queue.isEmpty()) {
        level++;
        int size = queue.size();
        for (int i = 0; i < size; i++) {
            TreeNode node = queue.poll();
            if (node.left == null && node.right == null) {
                return level;
            }
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
    }
    return level;
}

效率会高于之前后序遍历解法，因为找到第一个叶子节点后，就无需后续的层序遍历了

4.翻转二叉树-力扣 226 题

public TreeNode invertTree(TreeNode root) {
    fn(root);
    return root;
}

private void fn(TreeNode node){
    if (node == null) {
        return;
    }
    TreeNode t = node.left;
    node.left = node.right;
    node.right = t;
    fn(node.left);
    fn(node.right);
}

先交换、再递归或是先递归、再交换都可以

5.后缀表达式转二叉树

static class TreeNode {
    public String val;
    public TreeNode left;
    public TreeNode right;

    public TreeNode(String val) {
        this.val = val;
    }

    public TreeNode(TreeNode left, String val, TreeNode right) {
        this.left = left;
        this.val = val;
        this.right = right;
    }

    @Override
    public String toString() {
        return this.val;
    }
}

/*
    中缀表达式           (2-1)*3
    后缀（逆波兰）表达式   21-3*

    1.遇到数字入栈
    2.遇到运算符, 出栈两次, 与当前节点建立父子关系, 当前节点入栈

    栈
    |   |
    |   |
    |   |
    _____

    表达式树
        *
       / \
      -   3
     / \
    2   1

    21-3*
 */
public TreeNode constructExpressionTree(String[] tokens) {
    LinkedList<TreeNode> stack = new LinkedList<>();
    for (String t : tokens) {
        switch (t) {
            case "+", "-", "*", "/" -> { // 运算符
                TreeNode right = stack.pop();
                TreeNode left = stack.pop();
                TreeNode parent = new TreeNode(t);
                parent.left = left;
                parent.right = right;
                stack.push(parent);
            }
            default -> { // 数字
                stack.push(new TreeNode(t));
            }
        }
    }
    return stack.peek();
}

6.根据前序与中序遍历结果构造二叉树-力扣 105 题

• 先通过前序遍历结果定位根节点
• 再结合中序遍历结果切分左右子树

public class E09Leetcode105 {

    /*
        preOrder = {1,2,4,3,6,7}
        inOrder = {4,2,1,6,3,7}

        根 1
            pre         in
        左  2,4         4,2
        右  3,6,7       6,3,7


        根 2
        左 4

        根 3
        左 6
        右 7
     */

    public TreeNode buildTree(int[] preOrder, int[] inOrder) {
        if (preOrder.length == 0) {
            return null;
        }
        // 创建根节点
        int rootValue = preOrder[0];
        TreeNode root = new TreeNode(rootValue);
        // 区分左右子树
        for (int i = 0; i < inOrder.length; i++) {
            if (inOrder[i] == rootValue) {
                // 0 ~ i-1 左子树
                // i+1 ~ inOrder.length -1 右子树
                int[] inLeft = Arrays.copyOfRange(inOrder, 0, i); // [4,2]
                int[] inRight = Arrays.copyOfRange(inOrder, i + 1, inOrder.length); // [6,3,7]

                int[] preLeft = Arrays.copyOfRange(preOrder, 1, i + 1); // [2,4]
                int[] preRight = Arrays.copyOfRange(preOrder, i + 1, inOrder.length); // [3,6,7]

                root.left = buildTree(preLeft, inLeft); // 2
                root.right = buildTree(preRight, inRight); // 3
                break;
            }
        }
        return root;
    }

}

• 代码可以进一步优化，涉及新数据结构，以后实现

7.根据中序与后序遍历结果构造二叉树-力扣 106 题

• 先通过后序遍历结果定位根节点
• 再结合中序遍历结果切分左右子树

public TreeNode buildTree(int[] inOrder, int[] postOrder) {
    if (inOrder.length == 0) {
        return null;
    }
    // 根
    int rootValue = postOrder[postOrder.length - 1];
    TreeNode root = new TreeNode(rootValue);
    // 切分左右子树
    for (int i = 0; i < inOrder.length; i++) {
        if (inOrder[i] == rootValue) {
            int[] inLeft = Arrays.copyOfRange(inOrder, 0, i);
            int[] inRight = Arrays.copyOfRange(inOrder, i + 1, inOrder.length);

            int[] postLeft = Arrays.copyOfRange(postOrder, 0, i);
            int[] postRight = Arrays.copyOfRange(postOrder, i, postOrder.length - 1);

            root.left = buildTree(inLeft, postLeft);
            root.right = buildTree(inRight, postRight);
            break;
        }
    }
    return root;
}

• 代码可以进一步优化，涉及新数据结构，以后实现

8.在二叉树中分配硬币-力扣 979 题

给你一个有 n 个结点的二叉树的根结点 root ，其中树中每个结点 node 都对应有 node.val 枚硬币。整棵树上一共有 n 枚硬币。

在一次移动中，我们可以选择两个相邻的结点，然后将一枚硬币从其中一个结点移动到另一个结点。移动可以是从父结点到子结点，或者从子结点移动到父结点。

返回使每个结点上 只有 一枚硬币所需的 最少 移动次数。

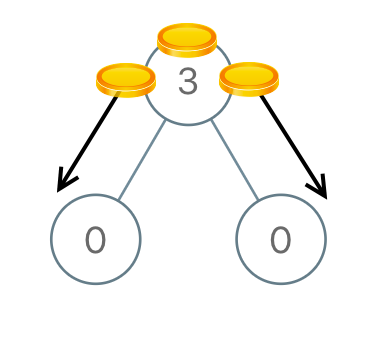
输入：root = [3,0,0]
输出：2
解释：一枚硬币从根结点移动到左子结点，一枚硬币从根结点移动到右子结点。

题解:

• 递归问题
• 将分配问题分解为硬币和节点的差值问题,不断地遍历
• 硬币总数为左右节点的硬币数量+当前节点的硬币数据量
• 节点数量为左右节点的数量+1(1 就是当前节点)

public class E11Leetcode979 {
    int res;

    public int distributeCoins(TreeNode root) {
        dfs(root);
        return res;
    }

    private int[] dfs(TreeNode root) {
        if (root == null) {
            //节点为空,则硬币数和节点数都为0
            return new int[]{0, 0};
        }
        final int[] dfsLeft = dfs(root.left);
        final int[] dfsRight = dfs(root.right);
        final int coins = dfsLeft[0] + dfsRight[0] + root.val;
        final int nodes = dfsLeft[1] + dfsLeft[1] + 1;
        res += Math.abs(coins - nodes);
        return new int[]{coins, nodes};
    }

    public static void main(String[] args) {
        E11Leetcode979 e11Leetcode979 = new E11Leetcode979();
        TreeNode root = new TreeNode(
                new TreeNode(new TreeNode(3), 0, new TreeNode(0))
                , 3
                , new TreeNode(new TreeNode(0), 0, new TreeNode(2))
        );
        System.out.println(e11Leetcode979.distributeCoins(root));
    }
}

9.二叉树的最近公共祖先-力扣 236 题

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

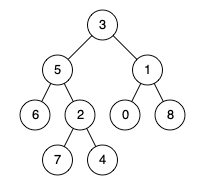
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

题解:

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    //找到就返回
    if (root == null || root == p || root == q) {
        return root;
    }
    //找左边
    TreeNode left = lowestCommonAncestor(root.left, p, q);
    //找右边
    TreeNode right = lowestCommonAncestor(root.right, p, q);
    //左边没有,则在右边
    if (left == null) {
        return right;
    }
    if (right == null) {
        return left;
    }
    //左右都有,则祖先就是root
    return root;
}

10.二叉树展开为链表-力扣 114 题

给你二叉树的根结点 root ，请你将它展开为一个单链表：

• 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
• 展开后的单链表应该与二叉树 先序遍历 顺序相同。

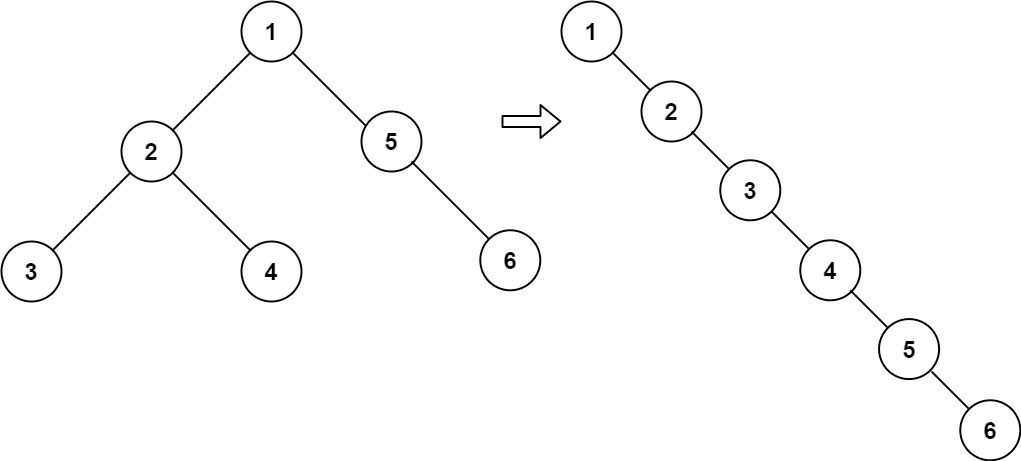
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

题解1:

public void flatten(TreeNode root) {
    //先序遍历
    List<TreeNode> list = new ArrayList<>();
    LinkedList<TreeNode> stack = new LinkedList<>();
    TreeNode curr = root;
    TreeNode pop = null;
    TreeNode  p = null;
    while (curr != null || !stack.isEmpty()) {
        if (curr != null) {
            list.add(curr);
            stack.push(curr);
            curr = curr.right;
        } else {
            final TreeNode peek = stack.peek();
            if (peek.left == null || peek.left == pop) {
                pop = stack.pop();
            } else {
                curr = peek.left;
            }
        }
    }
}

题解2:

public void flatten(TreeNode root) {
    LinkedList<TreeNode> stack = new LinkedList<>();
    TreeNode curr = root;
    TreeNode pre = null;
    while (curr != null || !stack.isEmpty()) {
        while (curr != null) {
            stack.push(curr);
            curr = curr.right;
        }
        curr = stack.peek();
        if (curr.left == null || curr.left == pre) {
            //弹出的节点
            curr = stack.pop();
            curr.left = null;
            //第一次右节点为null
            curr.right = pre;
            //把当前节点赋值为弹出节点
            pre = curr;
            curr = null;//为了弹出下一个元素
        } else {
            curr = curr.left;
        }
    }
}