# 一.优先级队列简介
# 1.无序数组实现
要点
- 入队保持顺序
- 出队前找到优先级最高的出队,相当于一次选择排序
public class PriorityQueue1<E extends Priority> implements Queue<E> {
Priority[] array;
int size;
public PriorityQueue1(int capacity) {
array = new Priority[capacity];
}
@Override // O(1)
public boolean offer(E e) {
if (isFull()) {
return false;
}
array[size++] = e;
return true;
}
// 返回优先级最高的索引值
private int selectMax() {
int max = 0;
for (int i = 1; i < size; i++) {
if (array[i].priority() > array[max].priority()) {
max = i;
}
}
return max;
}
@Override // O(n)
public E poll() {
if (isEmpty()) {
return null;
}
int max = selectMax();
E e = (E) array[max];
remove(max);
return e;
}
private void remove(int index) {
if (index < size - 1) {
System.arraycopy(array, index + 1,
array, index, size - 1 - index);
}
array[--size] = null; // help GC
}
@Override
public E peek() {
if (isEmpty()) {
return null;
}
int max = selectMax();
return (E) array[max];
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public boolean isFull() {
return size == array.length;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
- 视频中忘记了 help GC,注意一下
# 2.有序数组实现
要点
- 入队后排好序,优先级最高的排列在尾部
- 出队只需删除尾部元素即可
public class PriorityQueue2<E extends Priority> implements Queue<E> {
Priority[] array;
int size;
public PriorityQueue2(int capacity) {
array = new Priority[capacity];
}
// O(n)
@Override
public boolean offer(E e) {
if (isFull()) {
return false;
}
insert(e);
size++;
return true;
}
// 一轮插入排序
private void insert(E e) {
int i = size - 1;
while (i >= 0 && array[i].priority() > e.priority()) {
array[i + 1] = array[i];
i--;
}
array[i + 1] = e;
}
// O(1)
@Override
public E poll() {
if (isEmpty()) {
return null;
}
E e = (E) array[size - 1];
array[--size] = null; // help GC
return e;
}
@Override
public E peek() {
if (isEmpty()) {
return null;
}
return (E) array[size - 1];
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public boolean isFull() {
return size == array.length;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
# 3.堆实现
计算机科学中,堆是一种基于树的数据结构,通常用完全二叉树实现。堆的特性如下
- 在大顶堆中,任意节点 C 与它的父节点 P 符合 $P.value \geq C.value$
- 而小顶堆中,任意节点 C 与它的父节点 P 符合 $P.value \leq C.value$
- 最顶层的节点(没有父亲)称之为 root 根节点
例 1 - 满二叉树(Full Binary Tree)特点:每一层都是填满的
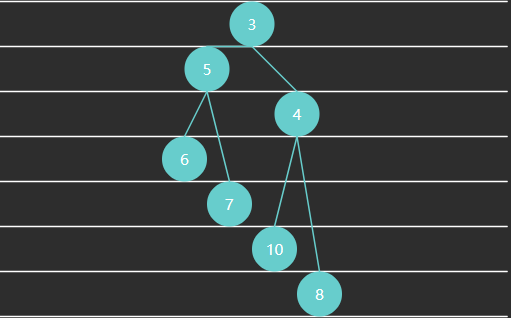
例 2 - 完全二叉树(Complete Binary Tree)特点:最后一层可能未填满,靠左对齐
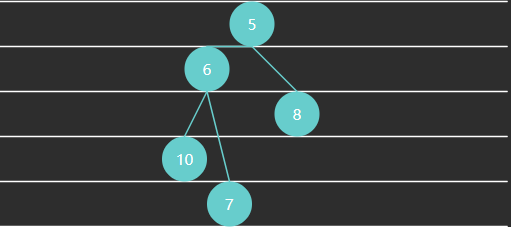
例 3 - 大顶堆
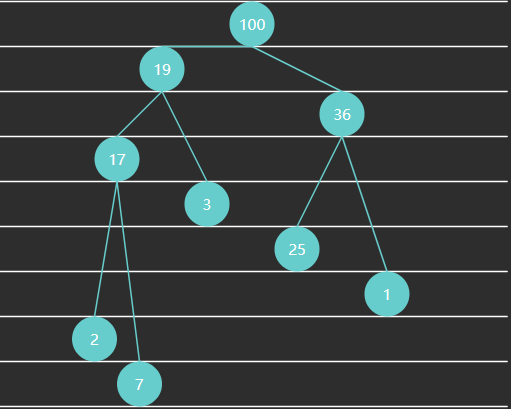
例 4 - 小顶堆
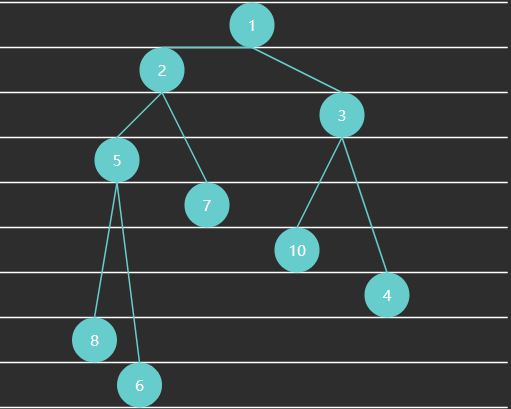
完全二叉树可以使用数组来表示
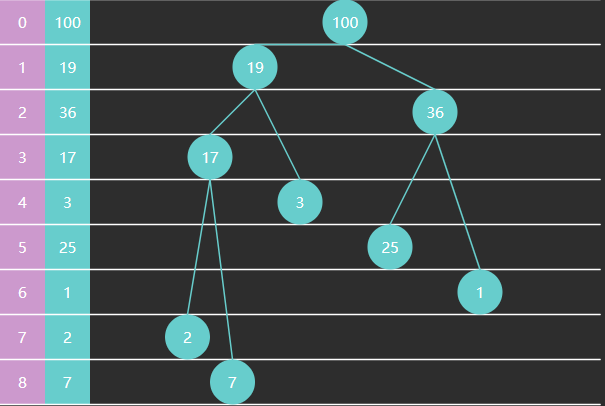
特征
- 如果从索引 0 开始存储节点数据
- 节点 $i$ 的父节点为 $floor((i-1)/2)$,当 $i>0$ 时
- 节点 $i$ 的左子节点为 $2i+1$,右子节点为 $2i+2$,当然它们得 $< size$
- 如果从索引 1 开始存储节点数据
- 节点 $i$ 的父节点为 $floor(i/2)$,当 $i > 1$ 时
- 节点 $i$ 的左子节点为 $2i$,右子节点为 $2i+1$,同样得 $< size$
代码
public class PriorityQueue4<E extends Priority> implements Queue<E> {
Priority[] array;
int size;
public PriorityQueue4(int capacity) {
array = new Priority[capacity];
}
@Override
public boolean offer(E offered) {
if (isFull()) {
return false;
}
int child = size++;
int parent = (child - 1) / 2;
while (child > 0 && offered.priority() > array[parent].priority()) {
array[child] = array[parent];
child = parent;
parent = (child - 1) / 2;
}
array[child] = offered;
return true;
}
private void swap(int i, int j) {
Priority t = array[i];
array[i] = array[j];
array[j] = t;
}
@Override
public E poll() {
if (isEmpty()) {
return null;
}
swap(0, size - 1);
size--;
Priority e = array[size];
array[size] = null;
shiftDown(0);
return (E) e;
}
void shiftDown(int parent) {
int left = 2 * parent + 1;
int right = left + 1;
int max = parent;
if (left < size && array[left].priority() > array[max].priority()) {
max = left;
}
if (right < size && array[right].priority() > array[max].priority()) {
max = right;
}
if (max != parent) {
swap(max, parent);
shiftDown(max);
}
}
@Override
public E peek() {
if (isEmpty()) {
return null;
}
return (E) array[0];
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public boolean isFull() {
return size == array.length;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
# 二.题目练习
# 1.合并多个有序链表-力扣 23 题
题目中要从小到大排列,因此选择用小顶堆来实现,自定义小顶堆如下
public class MinHeap {
ListNode[] array;
int size;
public MinHeap(int capacity) {
array = new ListNode[capacity];
}
public void offer(ListNode offered) {
int child = size++;
int parent = (child - 1) / 2;
while (child > 0 && offered.val < array[parent].val) {
array[child] = array[parent];
child = parent;
parent = (child - 1) / 2;
}
array[child] = offered;
}
public ListNode poll() {
if (isEmpty()) {
return null;
}
swap(0, size - 1);
size--;
ListNode e = array[size];
array[size] = null; // help GC
down(0);
return e;
}
private void down(int parent) {
int left = 2 * parent + 1;
int right = left + 1;
int min = parent;
if (left < size && array[left].val < array[min].val) {
min = left;
}
if (right < size && array[right].val < array[min].val) {
min = right;
}
if (min != parent) {
swap(min, parent);
down(min);
}
}
private void swap(int i, int j) {
ListNode t = array[i];
array[i] = array[j];
array[j] = t;
}
public boolean isEmpty() {
return size == 0;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
# 1.解法一
每次只对比 n 个,减少空间的消耗。
public class E01Leetcode23 {
public ListNode mergeKLists(ListNode[] lists) {
// 1. 使用 jdk 的优先级队列实现
// PriorityQueue<ListNode> queue = new PriorityQueue<>(Comparator.comparingInt(a -> a.val));
// 2. 使用自定义小顶堆实现
MinHeap queue = new MinHeap(lists.length);
for (ListNode head : lists) {
if (head != null) {
queue.offer(head);
}
}
ListNode s = new ListNode(-1, null);
ListNode p = s;
while (!queue.isEmpty()) {
ListNode node = queue.poll();
p.next = node;
p = node;
if (node.next != null) {
queue.offer(node.next);
}
}
return s.next;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
提问:
- 能否将每个链表的所有元素全部加入堆,再一个个从堆顶移除?
回答:
- 可以是可以,但对空间占用就高了,堆的一个优点就是用有限的空间做事情
# 2.解法二
将数据全部添加到优先级队列中,再逐个取出。
public ListNode mergeKLists(ListNode[] lists) {
MinHeap heap = new MinHeap(100);
// 1. 将链表的所有节点加入小顶堆
for (ListNode p : lists) {
while (p != null) {
heap.offer(p);
p = p.next;
}
}
// 2. 不断从堆顶移除最小元素, 加入新链表
ListNode s = new ListNode(-1, null);
ListNode curr = s;
while (!heap.isEmpty()) {
ListNode min = heap.poll();
curr.next = min;
curr = min;
curr.next = null; // 保证尾部节点指向 null
}
return s.next;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 3.解法三
使用 jdk 的优先级队列。
public ListNode mergeKLists(ListNode[] lists) {
PriorityQueue<ListNode> minHeap = new PriorityQueue<>((a, b) -> a.val - b.val);
for (ListNode p : lists) {
while (p != null) {
minHeap.add(p);
p = p.next;
}
}
ListNode s = new ListNode(-1, null);
ListNode p = s;
while (!minHeap.isEmpty()) {
p.next = minHeap.poll();
p = p.next;
}
return s.next;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public ListNode mergeKLists(ListNode[] lists) {
PriorityQueue<ListNode> minHeap = new PriorityQueue<>(Comparator.comparingInt(a -> a.val));
for (ListNode p : lists) {
while (p != null) {
minHeap.add(p);
p = p.next;
}
}
ListNode s = new ListNode(-1, null);
ListNode p = s;
while (!minHeap.isEmpty()) {
p.next = minHeap.poll();
p = p.next;
}
return s.next;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
